Трехфазное короткое замыкание в простейшей неразветвленной цепи.Составляющие тока короткого замыкания

Простейшей трехфазной цепью будем считать цепь без трансформаторных связей. Принимаем, что источник питания обладает бесконечной мощностью. На одной (левом) участке взаимоиндукция между фазами, на другом она отсутствует. Цепь присоединена к источнику синусоидального напряжения с неизменной амплитудой и частотой.

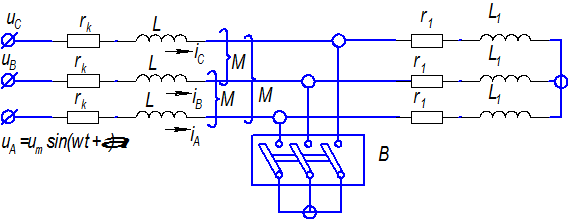
Рис. 1. Простейшая трехфазная электрическая цепь.

Переходный процесс вызывается включением выключателя В, на котором сделана закоротка, т.е. возникает металлическое трехфазное короткое замыкание между двумя участками цепи.

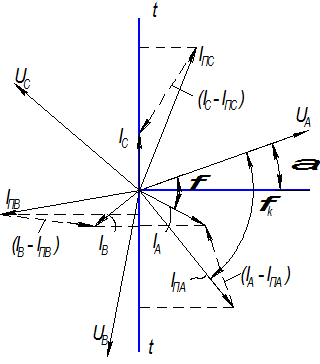
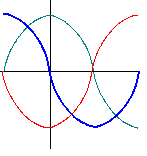
Рис.2. Векторная диаграмма для начального момента трехфазного короткого замыкания.

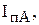
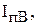
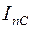- периодические составляющие, т.е. после короткого замыкания периодическая составляющая больше фазного тока до короткого замыкания и при ином угле φ. 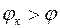. r после короткого замыкания уменьшилось, до короткого замыкания 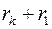, после короткого замыкания только 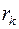. Следовательно, φ увеличится.

Пусть векторы 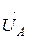, , 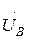, , 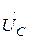, 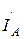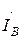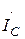- характеризуют предшествующий режим рассматриваемой цепи, а вертикаль t – t – неподвижная линия времени,. т.е. мгновенные значения отдельных величин определяются проекциями на эту линию соответствующих вращающихся векторов. Момент возникновения короткого замыкания определяется углом α (т.е. фазой включения) между вектором напряжения фазы А и горизонталью. (φ – угол сдвига в нормальном режиме). После включения выключателя В цепь распадается на два участка левый и правый независимые друг от друга. Правый участок зашунтирован коротким замыканием и ток в нем будет поддерживаться запасенной в индуктивности L электромагнитной энергией до тех пор, пока она не перейдет в тепло, поглощаемое активным сопротивлением. В каждой фазе правой части изменение тока описывается однородным дифференциальным уравнением:

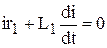(1)

Решение этого уравнения имеет вид:

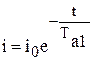(2)

Где 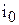- начальное значение тока рассматриваемой фазы;
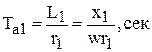- постоянная времени однофазной цепи.

Это решение показывает, что здесь имеется лишь свободный ток, который затухает по экспоненте с указанной постоянной времени.

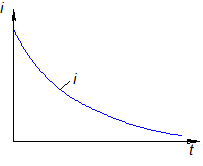
Нет источника питания.

Начальное значение свободного тока в каждой фазе зашунтированного участка цепи, очевидно, равно предшествующему мгновенному значению тока (первый закон коммутации i_L(0_)= i_L(0+)), поскольку в цепи с индуктивностью не может произойти внезапного изменения (скачка) тока. В общем случае свободные токи в фазах различны, хотя их затухания происходят с одной и той же постоянной времени. В одной из фаз свободный ток может вообще отсутствовать, если в момент возникновения короткого замыкания предшествующий ток в этой фазе проходит через нуль; при этом свободные токи в двух других фазах будут одинаковы по величине, но противоположны по направлению.

Перейдем теперь к участку цепи, который остался присоединенным к источнику. (Левая часть схемы). Здесь помимо свободного тока будет новый принудительный ток, величина которого больше предыдущего и сдвиг и сдвиг по фазе в общем случае иной. I_ПА, I_ПВ, I_ПС, φ_к.

Запишем дифференциальное уравнение равновесия для любой из фаз этого участка, например, фазы А. С учетом взаимной индуктивности контуров – коэффициент М – уравнение будет иметь вид:

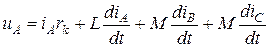(3)

Известно, что для трехпроводной системы:

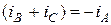
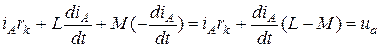
Если обозначить результирующую индуктивность фазы с учетом влияния двух других фаз 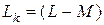, то для каждой из фаз можно записать (опуская индекс фазы А):

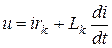(4)

Т.е. имеем линейное дифференциальное уравнение, а общий интеграл линейного дифференциального уравнения равен сумме частного решения неоднородного уравнения плюс полное решение однородного уравнения.

Однородное уравнение получаем из исходного (4), если в нем левую часть взять равной нулю:

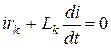(5)

Частное решение неоднородного уравнения равно .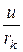

Поэтому решение линейного дифференциального уравнения можно записать в виде:

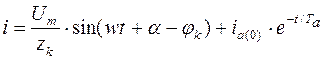(6)

где z_k – полное сопротивление присоединенного к источнику участка цепи, т.е. сопротивление цепи короткого замыкания;

φ_k – угол сдвига в этой цепи в режиме короткого замыкания;

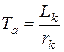- постоянная времени цепи короткого замыкания.

Первый член (слагаемое) правой части уравнения (или частное решение неоднородного дифференциального уравнения) называется принужденной составляющей тока и представляет периодическую слагаемую тока с постоянной амплитудой 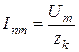. Второй член представляет собой (полное решение однородного уравнения) затухающий по экспоненте свободный ток или его называют апериодической слагающей тока. Начальное значение этой слагающей определяется из начальных условий, т.е.:

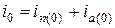(7)

где i₀ – полный ток, т.е. t=0.

Подставляя в это выражение начальное значение полного тока i₀ и его периодической составляющей 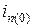можно найти .

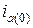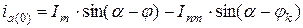(8)

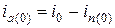
φ – начальный угол. Знак «-», т.к. ток отстает от напряжения на угол φ;

φ_к – т.к. появляется апериодическая составляющая после короткого замыкания. Знак «-», т.к. ток отстает от напряжения.

На векторной диаграмме принудительные токи будут выглядеть следующим образом.

Поскольку токи i_п и i₀ являются проекциями векторов 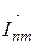и 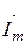на линию времени, то и ток 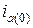можно рассматривать как проекцию вектора ( 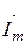- 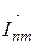) на ту же линию ( - ).

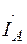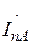Для практических целей важно определить максимальное возможное мгновенное значение тока короткого замыкания. Из предыдущего уравнения (8) следует, что наибольшее значение апериодической составляющей тока определяется не только фазой включения α, но также предшествующим режимом цепи. Так, например, при отсутствии предшествующего тока I_m=0 в цепи величина 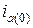может достигать амплитуды периодической слагающей 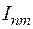, если в момент короткого замыкания эта слагающая (периодическая) проходит через свой положительный или отрицательный максимум. Обычно этот случай берется в качестве расчетного.

При отсутствии предшествующего тока (I_m=0) следует, что полный ток в цепи короткого замыкания является функцией двух независимых переменных: времени t и фазы включения α и выражается уравнением:

в (8) 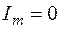, т.е.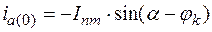

в (6) 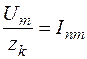. Следовательно, из (6) получаем:

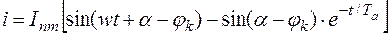(9)

Приравниваем к нулю частные производные этого уравнения, т.е.:

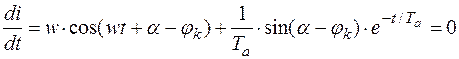(10)

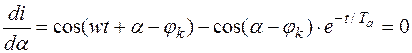(11)

Совместное решение этих уравнений показывает, что максимум тока наступает при :

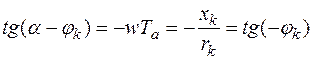
т.е. при α=0 (т.е. согласно рис.2 U_A проходит через 0). Следовательно, в предварительно разомкнутой цепи с r и L максимум мгновенного значения полного тока при коротком замыкании наступает, если в момент возникновения короткого замыкания напряжение источника проходит через нуль. Для цепи с преобладающей индуктивностью φ_к≈90⁰, поэтому условие возникновения максимума апериодической слагающей и условие, при котором достигается максимум мгновенного значения полного тока, очень близки друг к другу.

Дата добавления: 2014-12-09; просмотров: 1194; Нарушение авторских прав

Мы поможем в написании ваших работ!