Оценка качества уравнения регрессии

Прежде, чем построенное уравнение регрессии использовать в аналитических целях, оценивается его качество с помощью системы показателей: коэффициента корреляции, дисперсионного отношения Фишера, критерия Стьюдента.

Коэффициент корреляции показывает тесноту линейной связи между моделируемым показателем и фактором и рассчитывается по формуле

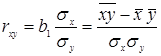, (1.3.1)

где

; .

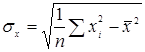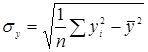Значение коэффициента корреляции заключены между -1 и 1. При 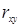=1 между показателем и фактором существует функциональная зависимость, при 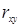=0 между показателем и фактором нет линейной связи, при 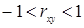имеет место корреляционная связь.

Квадрат коэффициента корреляции, умноженный на 100 ( 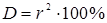), называют коэффициентом детерминации. Он показывает, насколько процентов вариация зависимой переменной y объясняется соответствующими изменениями независимой переменной x.

С помощью F-критерия (дисперсионного отношения Фишера) устанавливается адекватность регрессионной модели. Его расчет осуществляется по формуле

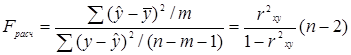, (1.3.2)

где

n – число элементов выборочной совокупности;

m – число факторов.

В числители критерия (1.3.2) стоит сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»), деленная на число степеней свободы m, а в знаменателе – остаточная сумма квадратов отклонений, деленная на (n-m-1) (остаточная дисперсия).

Если 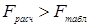, то построенная модель считается адекватной. 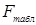- это максимально возможное значение дисперсионного отношения Фишера при данных степенях свободы и уровне значимости 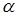. Обычно 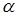принимается равным 0,05 или 0,01 и представляет собой вероятность отвергнуть правильную гипотезу при условии того, что она верна. Фактически, с помощью F-критерия проверяется 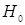- гипотеза о том, что 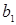=0.

Статистическая значимость каждого коэффициента регрессии в отдельности устанавливается с помощью t-критерия Стьюдента, рассчитываемого по формулам

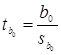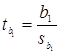; . (1.3.3)

Стандартные ошибки параметров линейной регрессии определяются по формулам

;

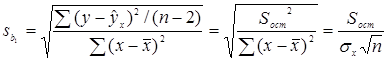(1.3.4)

.

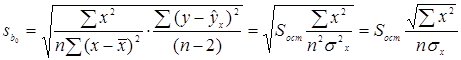Кроме критерия Стьюдента, стандартные ошибки используются при расчете предельных ошибок

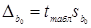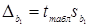; , (1.3.5)

которые, в свою очередь, применяются для определения доверительных интервалов.

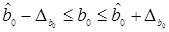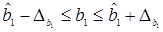; . (1.3.6)

Если границы доверительного интервала содержат 0, т.е. нижняя граница отрицательна, а верхняя – положительна, то оцениваемый параметр считается незначимым.

Дата добавления: 2015-01-19; просмотров: 267; Нарушение авторских прав

Мы поможем в написании ваших работ!