Содержательная интерпретация параметров регрессии

Если построенная модель адекватна, то становится правомерным ее практическое использование в аналитических целях. Практическое использование требует содержательной интерпретации результатов эконометрического моделирования.

Коэффициент линейной модели 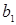является коэффициентом абсолютного роста. Он показывает на сколько единиц изменится показатель y, если фактор x изменится на 1.

В показательной модели 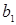является коэффициентом относительного роста. Он показывает во сколько раз изменится y, если x изменится на 1.

В степенной модели 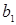является коэффициентом эластичности. Он показывает на сколько % изменится y, x изменится на 1 %.

Тест.

1. Какой вывод следует из равенства коэффициента корреляции 0?

1) между показателем и фактором нет зависимости;

2) между показателем и фактором нет линейной зависимости;

3) между показателем и фактором есть зависимость, но нелинейная.

2. Каковы возможные границы изменения коэффициента корреляции?

1) ;

2) ;

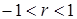3) .

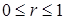3. Каковы возможные границы изменения индекса корреляции?

1) ;

2) ;

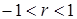3) .

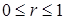4. В каком случае модель считается адекватной?

1) ;

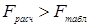2)

3) значение коэффициента корреляции >0,8.

5. Сравнимы ли между собой линейная и нелинейная модели по коэффициенту корреляции?

1) нет;

2) да;

3) сравнимы, если коэффициент корреляции рассчитан после приведения нелинейной модели к линейной форме.

6. Каким критерием необходимо пользоваться при выборе лучшей регрессионной модели?

1) коэффициентом корреляции между x и y;

2) суммой квадратов отклонений расчетных значений от фактических;

3) индексом корреляции.

7. Что следует предпринять, если значение коэффициента корреляции близко к 0?

1) принять решение об отсутствии связи между x и y;

2) перейти к построению многофакторной модели, включив в модель дополнительные факторы;

3) перейти к построению нелинейной модели.

8. Как интерпретируется в линейной модели коэффициент регрессии ?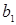

1) коэффициент эластичности;

2) коэффициент относительного роста;

3) коэффициент абсолютного роста.

9. Как в показательной модели интерпретируется коэффициент регрессии ?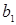

1) коэффициент эластичности;

2) коэффициент относительного роста;

3) коэффициент абсолютного роста.

10. Как в степенной модели интерпретируется коэффициент регрессии ?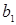

1) коэффициент эластичности;

2) коэффициент относительного роста;

3) коэффициент абсолютного роста.

11. Применим ли метод наименьших квадратов для расчета параметров нелинейных моделей?

1) нет;

2) да

3) применим после ее специального приведения к линейному виду.

12. Применим ли метод наименьших квадратов для расчета параметров показательной зависимости?

1) нет;

2) да;

3) применим после ее приведения к линейному виду путем логарифмирования.

13. Применим ли метод наименьших квадратов для расчета параметров степенной зависимости?

1) нет;

2) да;

3) применим после ее приведения к линейному виду путем логарифмирования.

14. Что показывает коэффициент абсолютного роста?

1) на сколько единиц изменится y, если x изменился на единицу;

2) на сколько процентов изменится y, если x изменился на один процент;

3) относительную величину изменения y при изменении x на единицу.

15. Что показывает коэффициент регрессии показательной модели?

1) на сколько единиц изменится y, если x изменился на единицу;

2) на сколько процентов изменится y, если x изменился на один процент;

3) относительную величину изменения y при изменении x на единицу.

16. Что показывает коэффициент регрессии степенной модели?

1) на сколько единиц изменится y, если x изменился на единицу;

2) на сколько процентов изменится y, если x изменился на один процент;

3) относительную величину изменения y при изменении x на единицу.

17. Какой коэффициент рассчитывается по формуле 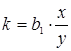в случае линейной зависимости?

1) коэффициент абсолютного роста;

2) коэффициент относительного роста;

3) коэффициент эластичности.

18. В каком случае линейная модель пригодна для использования в аналитических целях?

1) ;

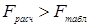2)

3) при отличии от нуля коэффициента корреляции.

19. Величина коэффициента абсолютного роста зависит в линейной модели 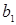от:

1) масштаба измерения y и x;

2) масштаба измерения только x;

3) не зависит.

20. Величина коэффициента эластичности зависит от:

1) масштаба измерения y и x;

2) масштаба измерения только x;

3) не зависит.

21. Какую модель следует выбрать, если есть основание считать, что в изучаемом периоде коэффициент абсолютного роста не изменяется?

1) линейную;

2) показательную;

3) степенную.

22. Какую модель следует выбрать, если есть основание считать, что в изучаемом периоде коэффициент относительного роста не изменяется?

1) линейную;

2) показательную;

3) степенную.

23. Какую модель следует выбрать, если есть основание считать, что в изучаемом периоде коэффициент эластичности не изменяется?

1) линейную;

2) показательную;

3) степенную.

24. Если коэффициент корреляции положителен, то в линейной модели:

1) с ростом x уменьшается y;

2) с ростом x увеличивается y;

3) с уменьшением x растет y.

25. Если коэффициент корреляции отрицателен, то в линейной модели:

1) с ростом x уменьшается y;

2) с ростом x увеличивается y;

3) с уменьшением x уменьшается y.

Дата добавления: 2015-01-19; просмотров: 583; Нарушение авторских прав

Мы поможем в написании ваших работ!