Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
Производная по направлению. Градиент
|
Читайте также: |
Пусть функция z = f (x, y) определена в некоторой окрестности точки М (х, у),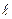 
- некоторое направление, задаваемое вектором 
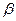- углы, образуемые вектором 
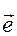с осями координат.
При перемещении точки М (х, у) в точку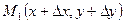 
в направлении 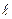функция z получит приращение 
, называемое приращением функции z в направлении .
У
 |
М1
 |
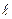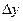
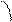
у 
 |
х Х
Производной 
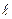по направлению функции двух переменных
z = f (x, y) называется предел:
Производная по направлению характеризует скорость изменения функций в направлении 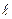. Можно показать, что
.
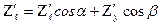Градиентом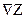 
функции z = f (x, y) называется вектор с координатами 
. Рассмотрим скалярное произведение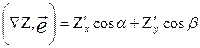 
. Отсюда видно, что производная по направлению равна скалярному произведению градиента 
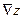и единичного вектора, задающего направление .
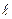Скалярное произведение двух векторов максимально, если векторы одинаково направлены. Следовательно, градиент функции в данной точке
характеризует направление максимальной скорости изменения функции в этой точке.
Теорема. Пусть задана дифференцируемая функция z = f (x, y) и пусть в точке М (х0, у0) величина градиента отлична от нуля. Тогда градиент перпендикулярен линии уровня, проходящей через данную точку.
| <== предыдущая страница | | | следующая страница ==> |
| | | Экстремум функции нескольких переменных |
Дата добавления: 2014-02-28; просмотров: 1208; Нарушение авторских прав
Мы поможем в написании ваших работ!