
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Производная функции
Пусть функция y =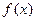 определена в окрестности точки x0,
определена в окрестности точки x0, 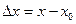 - приращение аргумента x,
- приращение аргумента x, 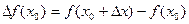 - приращение функции (рис 1а).
- приращение функции (рис 1а).
Определение 1. Производной функции 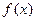 в точке x0 называется конечный предел
в точке x0 называется конечный предел 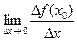 , если он существует.
, если он существует.
Производная функции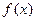 в точке x0 обозначается
в точке x0 обозначается 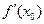 или
или 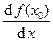 . Через y¢ или
. Через y¢ или 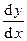 обозначают производную функции y =
обозначают производную функции y =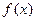 в точке x.
в точке x.
Замечание 1. Пусть предел в определении 1 равен +∞ (или – ∞). В этом случае говорят, что производная 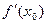 =+∞ (или – ∞).
=+∞ (или – ∞).
Определение 2.Если для любого достаточно малого Δx выполняется равенство
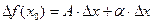 ,
,
где A - постоянная, α - бесконечно малая функция при Δx→0, то функция f(x) называется дифференцируемой в точке x0 (см. рис. 1а). Величина A∙Δx называется дифферециалом функции f(x) в точке x0 и обозначается символом df(x0). Дифферециал функции y = f(x) в точке x обозначается символом dy.
Теорема 1.Функция y = f(x) имеет в точке x (конечную) производную в том и только в том случае, если она дифференцируема в этой точке. При этом верно равенство
dy = f ′ (x) dx. (1)
В силу этой теоремы выражения “функция дифференцируема” и “функция имеет производную” означают одно и то же.
2. Таблица производных некоторых функций.
1. 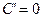 ( (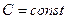 ) )
|
2. 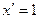
| 3. 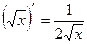
|
4. 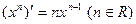
| 5. 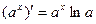
| 6. 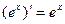
|
7. 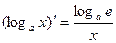
| 8. 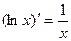
| 9. 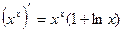
|
10. 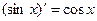
| 11. 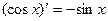
| 12. 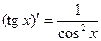
|
13. 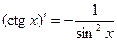
| 14. 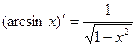
| 15. 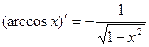
|
16. 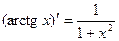
| 17. 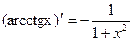
| 18. 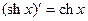
|
19. 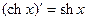
| 20. 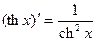
| 21. 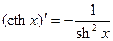
|
3. Действия над дифференцируемыми функциями.Пусть С – постоянная, 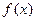 и
и 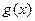 - дифференцируемые функции. Тогда
- дифференцируемые функции. Тогда
(1) (С f (x))¢ = С f ¢(x),
(2) 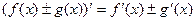 ,
,
(3) 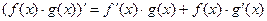 ,
,
(4) 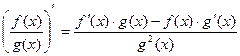 ,
, 
| <== предыдущая страница | | | следующая страница ==> |
| Точки разрыва функции | | |
Дата добавления: 2014-02-28; просмотров: 599; Нарушение авторских прав

Мы поможем в написании ваших работ!