Студопедия

Главная страница Случайная лекция


Мы поможем в написании ваших работ!

Порталы:

БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика



Мы поможем в написании ваших работ!




Экстремум функции нескольких переменных

Читайте также:
  1. III. Предмет, метод и функции философии.
  2. IV. По функции различают мышцы: сгибатели и разгибатели, отводящие и приводящие и вращатели.
  3. Бакампициллина - тяжелые нарушения функции печени, почек, беременность, лактация, детский возраст.
  4. Банковская система, ее структура. Функции Центрального банка. Операции коммерческих банков.
  5. Банковская система. Банки и их функции
  6. Бесконечно малые и бесконечно большие функции.
  7. Билет 13. Основные характеристики и функции чувств.
  8. Билет 13. Основные характеристики и функции чувств.
  9. Билет 28. Общение, его функции и структура.
  10. Биологическая и социальная функции отвращения

 

Точка М (х0, у0) называется точкой максимума (минимума) функции

z = f (x, y), если существует окрестность точки М такая, что для всех точек

(x, y) из этой окрестности выполняется неравенство:

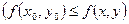
Теорема (многомерный аналог теоремы Ферма). Пусть точка (х0, у0) – точка экстремума дифференцируемой функции z = f (x, y). Тогда частные производные 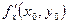и в этой точке равны нулю.

Точки, в которых частные производные равны нулю, называются критическими или стационарными.

В точке минимума или максимума дифференцируемой функции градиент равен нулю. Кроме того, в точке экстремума обращаются в нуль производные функции по всем направлениям.

Равенство нулю частных производных выражает лишь необходимое, но не достаточное условие экстремума функции нескольких переменных.

Пример – седловая точка. Здесь 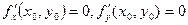, но никакого экстремума в точке М (х0, у0) нет. Седловые точки являются двумерными аналогами точек перегиба функций одной переменной.

Чтобы определить точки экстремума, нужно достаточное условие экстремума. Для этого определим частные производные 2-го порядка. Если 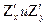сами являются дифференцируемыми функциями, то можно найти и их частные производные, которые называются частными производными 2-го порядка: .

Если частные производные 2-го порядка непрерывны в точке М (х0, у0), то в этой точке .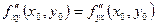

Теорема (достаточное условие экстремума). Пусть функция z = f (x, y) определена в некоторой окрестности критической точки (х0, у0) и имеет в этой точке непрерывные частные производные 2-го порядка: . Тогда , если , то в точке (х0, у0) функция имеет экстремум, причем A < 0 – максимум, при

A > 0 – минимум. В случае 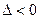функция эктремума не имеет. Если 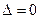, то вопрос о наличии эктремума остается открытым.

Схема исследования функции двух переменных на экстремум:

1. Найти частные производные и .

2. Решить систему уравнений и найти критические точки функции.

3. Найти частные производные 2-го порядка, вычислить их значение в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.

4. Найти экстремальное значения функции.

 

Вопросы для самоконтроля знаний:

1. Применение функции нескольких переменных в экономике.

2. Условный экстремум. Метод множителей Лагранжа.

 

Литература

Основная:

1. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер и др. - М.: ЮНИТИ, 2010. - 471с.

2. Высшая математика для экономистов: Практикум для Вузов / Н.Ш. Кремер и др.– М.: ЮНИТИ, 2010. - 471с.

3. Кытманов А.М. Математический анализ: учебное пособие для бакалавров / А.М. Кытманов. – М.: Издательство Юрайт, 2014. – 607 с.

Дополнительная:

1. Попов А.М. Высшая математика для экономистов: учебник для бакалавров / А.М. Попов, В.Н. Сотников.– М.: Издательство Юрайт, 2012.– 564 с.

2. Общий курс высшей математики для экономистов / Под ред. И.Ермакова. – М.: ИНФРА-М, 2009 г. – 656 с.

 

 
<== предыдущая страница | следующая страница ==>
Производная по направлению. Градиент | Организация пассажирских перевозок (11.02.14)

Дата добавления: 2014-02-28; просмотров: 726; Нарушение авторских прав



Мы поможем в написании ваших работ!
lektsiopedia.org - Лекциопедия - 2013 год. | Страница сгенерирована за: 0.007 сек.