Графическое решение линейного неравенства

Рассмотрим линейное неравенство с двумя переменными .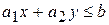

· Решением линейного неравенства с двумя переменными

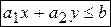
называется множество пар значений переменных 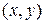, которые удовлетворяют неравенству.

· Геометрическим решением линейного неравенства

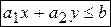
является множество точек на плоскости, лежащих по одну сторону от граничной прямой 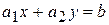. Это множество образует полуплоскость, границей которой является прямая .

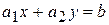Порядок действий для графического решения линейного неравенства 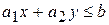(построения полуплоскости):

1) записать уравнение граничной прямой 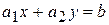и построить на плоскости эту прямую (по двум точкам);

2) выбрать искомую полуплоскость, координаты точек в которой удовлетворяют заданному неравенству.

Для выбираем точку с известными координатами 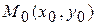, не лежащую на граничной прямой. Подставляем в неравенство 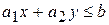координаты точки 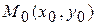. Если получится верное числовое неравенство, то искомая полуплоскость та, которая содержит точку 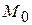. Полуплоскость выделяется штриховкой в сторону точки 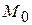. Если же при подстановке получится неверное числовое неравенство, то искомая полуплоскость та, которая не содержит точку 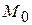. Решением неравенства будет та полуплоскость, которая не содержит точку 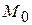. Штриховка отмечается в ту сторону, которая не содержит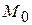

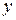
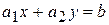
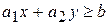
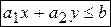
0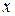

Отметим, что неравенство 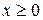определяет правую координатную полуплоскость (от оси 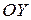), а 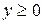- верхнюю координатную полуплоскость (от оси ).

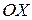Пример. Решить графически неравенство .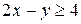

Запишем уравнение граничной прямой 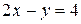и построим ее по двум точкам, например, 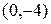и 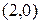. Прямая делит плоскость на две полуплоскости.

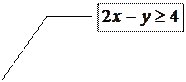
0 2

-4

Координаты точки 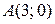удовлетворяют неравенству 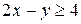( 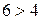– верно), значит, и координаты всех точек полуплоскости, содержащей точку 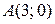, удовлетворяют неравенству.

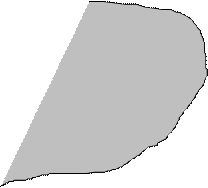
Решением неравенства будут координаты точек полуплоскости, расположенной справа от граничной прямой 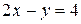, включая точки на границе. Искомая полуплоскость на рисунке выделена.

Дата добавления: 2015-06-30; просмотров: 268; Нарушение авторских прав

Мы поможем в написании ваших работ!