
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Неравенство треугольника
|
Читайте также: |
Для изучения последней темы раздела нам потребуется:
1. Вспомнить аксиому измерения отрезков. Сформулируйте ее.
2. Знать несколько свойств неравенств, которые мы подробно будем изучать на уроках алгебры в конце 8 класса. Запишем их (на доске и в тетрадях) для знака «>» (для знаков «<», «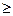 », «
», «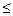 » - аналогично).
» - аналогично).
а) 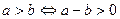 ; б)
; б) 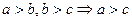 ; в)
; в) 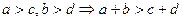 ;
;
г) 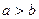 и
и 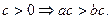
3. Сформулировать полностью определение. Расстоянием между точками А и В называется: |AB|, если А и В — различны; число 0, если А = В.
4. стр. 106 — 107, теорема — прочитайте формулировку (вслух).
Доказательство прочитайте самостоятельно.
Вопросы:
а) Докажите утверждение теоремы для случая 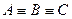 [неравенство
[неравенство 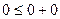 истинно]
истинно]
б) Докажите утверждение теоремы для случая совпадения двух точек, например,  [неравенства
[неравенства 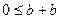 и
и 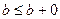 истинны]
истинны]
в) Какой еще случай рассматривается отдельно и что применяется для доказательства? [точки А, В и С лежат на одной прямой; аксиома измерения отрезков]
Почему в этом случае расстояние между любыми двумя точками не превосходит суммы двух других расстояний? [сумма положительных слагаемых больше каждого из них]
г) Почему при рассмотрении основного случая (АВС — треугольник) записано, что 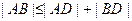 , а не |AB| = |AD| + |BD|? [углы А или В могут быть тупыми]
, а не |AB| = |AD| + |BD|? [углы А или В могут быть тупыми]
Можно ли в заключительной фазе рассуждения в этом случае записать вместо знака «<» знак ≤? [да, так как 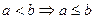 ]
]
Доказанное свойство попарных расстояний между тремя точками называется неравенством треугольника. Его принято записывать так: 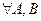 и
и 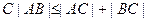
Далее учитель обобщает изученное, выделяет главное.
| <== предыдущая страница | | | следующая страница ==> |
| Перпендикуляр и наклонная | | | Устное решение задач |
Дата добавления: 2014-03-01; просмотров: 406; Нарушение авторских прав

Мы поможем в написании ваших работ!