Перпендикуляр и наклонная

Изучение новой темы.

Ученики по ходу рассказа учителя делают рисунки и основные записи в тетради (то, что учитель оформляет на доске).

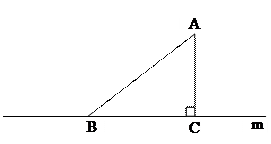1) Рассмотрим прямую m и точку А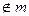(см. рисунок на доске и в тетрадях). Проведем 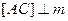, 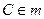. Как называются: [AC]? Точка С? [перпендикуляр к прямой m; основание перпендикуляра]. Сколько перпендикуляров можно провести из данной точки к данной прямо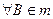й? и 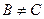, [AB]— наклонная к прямой m; В — основание наклонной; [BC] — проекция этой наклонной, то есть, отрезок, соединяющий основания перпендикуляра и наклонной. Сколько наклонных можно провести из точки А к данной прямой? Сравните длину любой и наклонной с длиной перпендикуляра.

Сформулируйте соответствующее свойство наклонной и докажите его. [Если из одной точки к прямой проведены перпендикуляр и наклонная, то длина наклонной больше длины перпендикуляра]

Доказав это свойство, мы объяснили, почему расстоянием от точки до прямой является длина перпендикуляра, опущенного на прямую из этой точки, а не длина какого-то другого отрезка. В геометрии в качестве расстояния между фигурами принято брать расстояние между их ближайшими точками!

2) Сколько равных наклонных можно провести к прямой m из точки А? Почему? [Две, так как окружность и прямая не могут иметь более двух общих точек, см. рисунок]. Как построить их проекции? Как связаны длины проекций равных наклонных? Верно ли обратное?

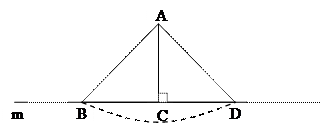Теорема. Наклонные, проведенные из данной точки к данной прямой равны тогда и только тогда, когда равны их проекции.

Дано: 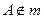; 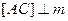, 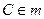. [AB] и [AD] — наклонные к m

Доказать: .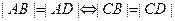

Доказательство: 1) Если |AB| = |AD|, то [AC] — высота в равнобедренном ΔBAD, проведенная к основанию, следовательно, [AC] — медиана, то есть, |CB| = |CD|, ч.т.д.

2) Если |CB| = |CD|, то [AC] — высота и медиана в ΔBAD, значит он — равнобедренный, то есть, |AB| = |AD|, ч.т.д.

Какие еще условия равносильны сформулированным? [Равенство углов между наклонными и проекциями или равенство углов между наклонными и перпендикуляром]

3) Как связаны проекции двух не равных наклонных, проведенных к прямой из данной точки? Верно ли обратное утверждение?

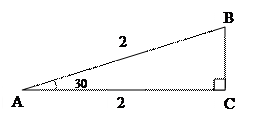Теорема. Из двух наклонных, проведенных из данной точки к данной прямой, одна больше тогда и только тогда, когда больше ее проекция.

Дано: 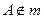; 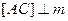, 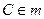[AB] и [AD] — наклонные к m

Доказать: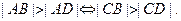

Доказательство. По теореме Пифагора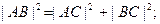

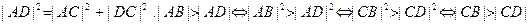, ч.т.д.

Вопросы. 1) Является ли зависимость между длинами наклонной и ее проекции прямой пропорциональностью? [Нет]

2) Как изменяется острый угол между наклонной и а) данной прямой; б) перпендикуляром к данной прямой по мере увеличения длины наклонной? [а) уменьшается; б) увеличивается]

3) Почему в обеих рассмотренных теоремах подчеркивается, что наклонные проведены к данной прямой из одной точки? [контр примеры показать на доске]

Дата добавления: 2014-03-01; просмотров: 960; Нарушение авторских прав

Мы поможем в написании ваших работ!