Перпендикулярные геометрические объекты

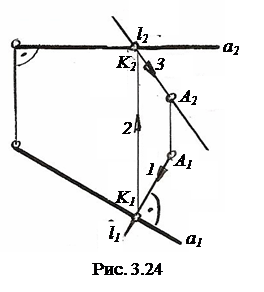3.5.1. Перпендикулярные прямые.На рис. 3.24 показано построение прямой ℓ, проходящей через точку Aиперпендикулярной прямой a.

Прямая a-горизонталь, то есть a||Π₁.

Из теоремы о частном случае проецирования прямого линейного угла (см. рис. 1.10) следует, что если одна сторона прямого линейного угла параллельна какой-либо плоскости проекций, то на эту плоскость прямой угол спроецируется в натуральную величину.

Следовательно, через A₁ проводим ℓ₁┴a₁, отмечаем точку K₁, находим K₂ по линии проекционной связи на a₂ и проводим ℓ₂, то есть ℓ₁┴a₁ так как a||Π₁ и ℓ┴a (рис. 3.24).

3.5.2. Перпендикулярные прямая и плоскость.Как известно, прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, лежащим в этой плоскости.

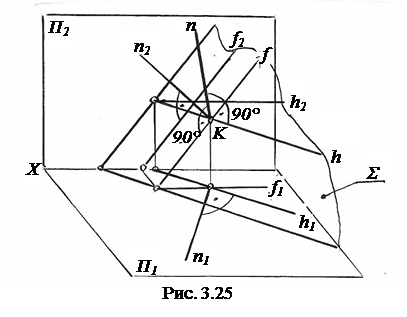При построениях удобно применять в качестве пересекающихся прямых горизонталь h и фронталь f.

Пусть необходимо (рис. 3.25) из точки K 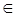Σ восставить перпендикуляр n ^ Σ.

Для этого через точку K проведём горизонталь h и фронталь f и перпендикулярно к ним проведём прямую n (n┴h и n┴f).

На основании теоремы о частном случае проецирования прямого линейного угла угол между n и h на Π₁ спроецируется без искажения, то есть угол между горизонтальной проекцией горизонтали h₁ и горизонтальной проекцией перпендикуляра n₁ будет прямым (n₁┴h₁).

Аналогичным образом можно доказать, что если n┴f, то n₂┴f₂, где

f₂ – фронтальная проекция фронтали.

Следовательно, если прямая перпендикулярна к плоскости, то её проекции перпендикулярны к одноимённым проекциям одноимённых линий уровня, то есть если n┴ Σ (h∩f), то n₁┴h₁ и n₂┴f₂.

Пусть требуется из точки K(K₁, K₂)восстановить перпендикуляр к плоскости Σ (a||b)(рис. 3.26, а).

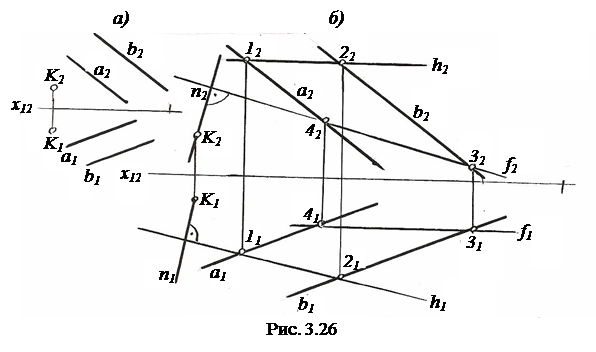На рис. 3.26, б показано построение такого перпендикуляра .

В плоскости Σ проведены горизонталь h (h₁, h₂) и фронталь f (f₁, f₂).

Через точку K₁ проведена n₁┴h₁ и через точку K₂ проведена n₂┴f₂.

3.5.3. Перпендикулярные плоскости. Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую линию, перпендикулярную другой. Поэтому при проведении плоскости, перпендикулярной к другой плоскости, сначала строят прямую, перпендикулярную к плоскости, и затем заключают её в какую-либо плоскость.

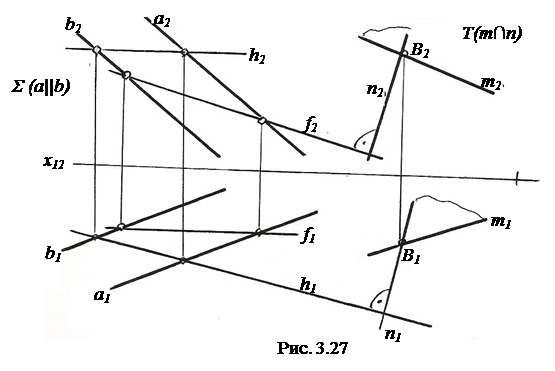
На рис. 3.27 через точку B проведена плоскость T(m∩n) перпендикулярно Σ (a||b).

Для этого в плоскости Σ (a||b) построены горизонталь h (h₁, h₂) и фронталь f (f₁, f₂).

Затем через точку B проводим n┴Σ, то есть n₁┴h₁, n₂┴f₂. Прямую m (m₁, m₂) через точку B (B₁ , B₂) проводим произвольно.

Построенная плоскость T (m∩n) будет перпендикулярна Σ.

Дата добавления: 2014-09-26; просмотров: 401; Нарушение авторских прав

Мы поможем в написании ваших работ!