Метод Монте-Карло

Во многих задачах исходные данные носят случайный характер, поэтому для их ре­шения должен применяться статистико-вероятностный подход. На основе таких подходов построен ряд числен­ных методов, которые учитывают случайный характер вычисляемых или измеряемых величин. К ним принад­лежит и метод статистических испытаний, называемый также методом Монте-Карло, который применяется к ре­шению некоторых задач вычислительной математики, в том числе и для вычисления интегралов.

Метод Монте-Карло состоит в том, что рассматрива­ется некоторая случайная величина , математическое ожидание которой равно искомой величине : .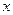

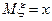Проводится серия 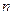независимых испытаний, в резуль­тате которых получается (генерируется) последователь­ность 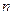случайных чисел 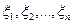, и по совокупно­сти этих значений приближенно определяется искомая величина

, .

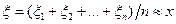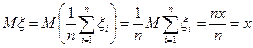Пусть 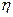- равномерно распределенная на отрезке 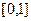случайная величина. Это означает, что ее плотность распределения задается соотношением

.

Тогда любая функция 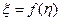также будет случайной величиной, и ее математическое ожидание равно

.

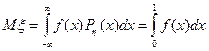Следовательно, читая это равенство в обратном порядке, приходим к выводу, что интеграл может быть вычислен как математическое ожидание некоторой случайной величины , которая определяется независи­мыми реализациями случайной величины 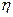с равно­мерным законом распределения:

.

Аналогично могут быть вычислены и кратные инте­гралы. Для двойного интеграла получим

,

Где 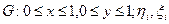- независимые реализа­ции случайных величин 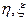, равномерно распределенных на отрезке .

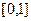Для использования метода Монте-Карло при вычис­лении определенных интегралов, как и в других его при­ложениях, необходимо вырабатывать последовательности случайных чисел с заданным законом распределения. Существуют различные способы генерирования таких чисел.

Можно построить некоторый физический процесс (ге­нератор) для выработки случайных величин, однако при использовании ЭВМ этот способ непригоден, поскольку трудно дважды получить одинаковые совокупности слу­чайных чисел, которые необходимы при отладке про­грамм.

Известны многие таблицы случайных чисел, которые вычислялись независимо. Их можно вводить в ЭВМ, хра­нить в виде файла на магнитной ленте или магнитном диске коллективного пользования. А еще лучше загото­вить собственный файл случайных чисел.

В настоящее время наиболее распространенный спо­соб выработки случайных чисел на ЭВМ состоит, в том, что в памяти хранится некоторый алгоритм выработки таких чисел по мере потребности в них (подобно тому, как вычисляются значения элементарных функций, а не хранятся их таблицы). Поскольку эти числа генериру­ются по наперед заданному алгоритму, то они не совсем случайны (псевдослучайны), хотя и обладают свойствен­ными случайным числам статистическими характеристи­ками.

Дата добавления: 2014-03-01; просмотров: 550; Нарушение авторских прав

Мы поможем в написании ваших работ!