Погрешность численного дифференцирования

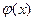Ап­проксимируем функцию некоторой функцией , т. е. представим ее в виде

(7).

В качестве аппроксимирующей функции 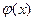можно принять частичную сумму ряда или интерполяционную функцию. Тогда погрешность аппроксимации 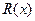опре­деляется остаточным членом ряда или интерполяционной формулы.

Аппроксимирующая функция 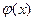может быть ис­пользована также для приближенного вычисления производной функции . Дифференцируя равенство (7) необходимое число раз, можно найти значения производ­ных :

, .

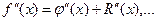В качестве приближенного значения производной по­рядка 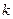функции можно принять соответствующее значение производной функции 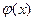, т. е.

.

Величина 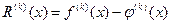, характеризующая отклонение приближенного значения производной от ее истинного значения, называется по­грешностью аппроксимации производной.

При численном дифференцировании функции, задан­ной в виде таблицы с шагом 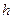, эта погрешность зависит от 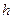, и ее записывают в виде 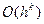. Показатель степени 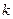называется порядком погрешности аппроксимации про­изводной (пли просто порядком аппроксимации). При этом предполагается, что значение шага по модулю меньше единицы.

Оценку погрешности легко проиллюстрировать с по­мощью ряда Тейлора

.

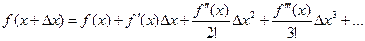Пусть функция задана в виде таблицы 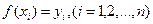. Запишем ряд Тейлора при с точностью до членов порядка :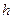

.

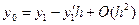Отсюда найдем производной в точке :

.

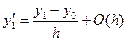Это выражение совпадает с формулой (3), которая, как видно, является аппроксимацией первого порядка (). Аналогично, записывая ряд Тейлора при 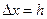, можно получить аппроксимацию (4). Она также имеет первый порядок.

Используем теперь ряд Тейлора для оценки погреш­ностей аппроксимаций (5) и (6). Полагая 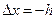и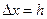, соответственно получаем

(8).

Вычитая эти равенства одно из другого, после очевид­ных преобразований получаем

.

Это аппроксимация производной (5) с помощью цент­ральных разностей. Она имеет второй порядок.

Складывая равенства (8), находим оценку погреш­ности аппроксимации производной второго порядка ви­да (6):

.

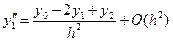Таким образом, эта аппроксимация имеет второй порядок. Аналогично можно получить аппроксимации производных более высоких порядков и оценку их погрешностей.

Мы рассмотрели лишь один из источников погрешно­сти численного дифференцирования - погрешность ап­проксимации (ее также называют погрешностью усече­ния). Она определяется величиной остаточного члена.

Анализ остаточного члена нетривиален, и сведения по этому вопросу можно найти в более полных курсах по численным методам и теории разностных схем. Отметим лишь, что погрешность аппроксимации при уменьшении шага 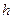, как правило, уменьшается.

Погрешности, возникающие при численном дифферен­цировании, определяются также неточными значениями функции в узлах и погрешностями округлений при проведении расчетов на ЭВМ. В отличие от погрешности аппроксимации погрешность округления возрастает с уменьшением шага 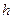. Поэтому суммарная погрешность численного дифференцирования может убывать при уменьшении шага лишь до некоторого предельного зна­чения, после чего дальнейшее уменьшение шага не по­высит точности результатов.

Оптимальная точность может быть достигнута за счет регуляризации процедуры численного дифференцирова­ния. Простейшим способом регуляризации является такой выбор шага 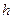, при котором справедливо неравенство 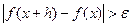, где - некоторое малое число. При вычислении производной это исключает вычитание близких по величине чисел, которое обычно приводит к увеличению погрешности. Это тем более опасно при по­следующем делении приращения функции на малое чис­ло 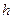. Другой способ регуляризации — сглаживание таб­личных значений функции подбором некоторой гладкой аппроксимирующей функции, например многочлена.

Использование интерполяционных формул.

Предпо­ложим, что функция , заданная в виде таблицы с постоянным шагом 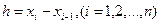, может быть аппроксимирована интерполяционным многочленом Ньютона (3):

,

.

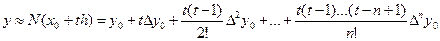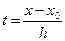Дифференцируя этот многочлен по переменной 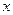с уче­том правила дифференцирования сложной функции:

,

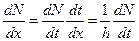можно получить формулы для вычисления производных любого порядка:

Интерполяционные многочлены Ньютона (а также Стирлинга и Бесселя) дают выражения для производных через разности 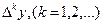. Однако на практике часто выгоднее выражать значения производных не через разности, а непосредственно через значения функции в узлах. Для получения таких формул удобно воспользо­ваться формулой Лагранжа с равномерным расположени­ем узлов .

Таблица 1.

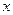
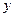
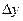
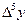
	1,2833
0,1	1,8107	0,5274
0,2	2,3606	0,5599	0,0325
0,3	2,9577	0,5971	0,0372	0,0047
0,4	3,5969	0,6392	0,0421	0,0049	0,0002
0,5	4,2833	0,6864	0,0472	0,0051	0,0002	0,000

Запишем интерполяционный многочлен Лагранжа и его остаточный член для случая трех узлов интерполяции () и найдем их производные:

.

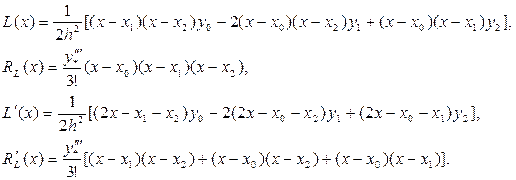Здесь 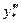- значение производной третьего порядка в некоторой внутренней точке .

Запишем выражение для производно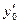й при :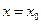

Аналогичные соотношения можно получить и для значений при :

.

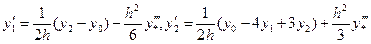Записывая интерполяционный многочлен Лагранжа и его остаточный член для случая четырех узлов (), получаем следующие аппроксимации производных:

(9).

В случае пяти узлов (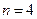) получим:

(10).

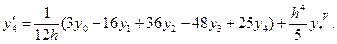
Таким образом, используя значения функции в 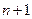узлах, получаем аппроксимацию производных 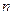-го поряд­ка точности. Эти формулы можно использовать не только для узлов 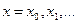, но и для любых узлов 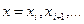, соответствующим образом изменяя значения индексов.

Обратим внимание на то, что при четных 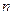наиболее простые выражения и наименьшие коэффициенты в оста­точных членах получаются для производных в средних (центральных) узлах ( при при 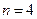и т. д.). Выпишем аппроксимации производных для узла с произ­вольным номером 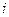, считая его центральным:

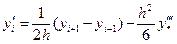, , (11)

, .

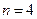Они называются аппроксимациями производных с по­мощью центральных разностей и широко используются на практике.

С помощью интерполяционных многочленов Лагранжа можно получить аппроксимации для старших производ­ных. Приведем аппроксимации для вторых производных.

В случае трех узлов интерполяции () имеем

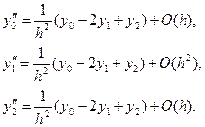(12).

В случае четырех узлов интерполяции () имеем

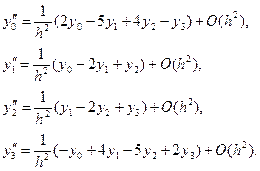(13).

Аппроксимации вторых производных с помощью центральных разностей при четных 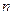также наиболее выгодны.

Дата добавления: 2014-03-01; просмотров: 848; Нарушение авторских прав

Мы поможем в написании ваших работ!