
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Сетевой метод
Сущность сетевого планирования состоит в составлении информационно-динамической, логико-математической модели заданного объекта в виде сетевого графика, в котором отражаются взаимосвязь и длительность определенного комплекса работ.
Сетевые модели отличаются большим разнообразием. Классифицируются модели в зависимости от:
1) объема охватываемых работ (большие сети, средние и малые)
2) количества целей (одноцелевые и многоцелевые)
3) степени детализации (укрупненные и конкретизированные)
4) степени неопределенности их структуры (детерминированные, стохастические, смешанные)
5) иерархического уровня (первичные, частные, сводные).
Сетевое планирование позволяет наглядно представить взаимосвязи между отдельными элементами системы, определить те работы, которые лимитируют выполнение других работ и всего плана в целом.
План в данном виде планирования отражается в виде сетевого графа, т.е. сетевой модели. В сетевой модели весь комплекс мероприятий по достижению цели расчленяется на четко определенные операции, которые располагаются в технологической последовательности их выполнения во взаимной связи и завершаются промежуточными и конечными результатами.
Основные элементы сетевой модели: работа, событие, путь.
Работа – прием, действие, естественный процесс, логическая зависимость, выполняемые в неизменных условиях и приводящие к однозначно понимаемому результату. Отражается стрелкой. Различают несколько видов работы: действительная работа, ожидание, зависимость (фиктивная работа). Действительная работа – процесс, требующий затрат времени и ресурсов. Ожидание – процесс, требующий только затрат времени и не нуждающийся в использовании ресурсов. Зависимость (фиктивная работа) – логическая связь между двумя или несколькими событиями, которая не требует ни времени, ни ресурсов для своего осуществления. Этот вид работы указывает только на то, что определенное событие не может начаться без осуществления другого события. Первых два вида работ отражается сплошной стрелкой, третий – пунктирной стрелкой. Всякая работа, кроме логической связи, является действием, которое нужно выполнить. Она может иметь характеристику затрат времени, труда, материальных и финансовых ресурсов. Главным показателем работы в сетевой модели является время, длительность ее выполнения. Поэтому над стрелкой указывается длительность выполнения работы.
Событие – однозначно понимаемые всеми результат выполнения работ. Это момент времени, определяющий возможность осуществления работы или нескольких работ. Событие является разграничителем плана работ, т.к. является результатом выполнения предшествующей работы и необходимым условием начала последующей. Продолжительность события во времени равна нулю. Событие обозначается кружком, внутри которого ставится номер события.
Событие обозначается номером или цифровым шифром. В этом случае каждая работа обозначается шифрами начального и конечного события в виде пары индексов (ij).
В зависимости от числа работ, которые заканчиваются данным событием, и количества работ, начинающихся с него, событие может быть простым и сложным.
Крайне важно правильно формулировать название работ и событий. Точная формулировка способствует тому, что внимание руководителей направляется не только на достижение конечной цели, но и на то, чем должна закончиться каждая работа, каков ее результат для того, чтобы могла начаться следующая работа. Особенно это важно тогда, когда работы выполняются разными отделами и исполнителями.
В сетевой модели существуют события особого вида, которые являются начальными и конечными для всего комплекса работ. Исходное событие – то, с которого начинается сеть. Оно представляет собой формулировку условий для начала всех работ по данному комплексу. Оно обозначается нулем или единицей и не имеет предшествующих работ. Завершающее событие представляет собой формулировку цели всего комплекса работ. Оно не является условием начала ни одной из работ, входящих в данную сеть. Для многоцелевых сетей характерно наличие нескольких завершающих событий.
Путь – непрерывная технологическая последовательность работ в сети. Конечное событие каждой работы в пути совпадает с начальным событием одной следующей за ней работы. Путь часто задается последовательным перечислением номеров лежащих на нем событий. Следует различать полный и неполный (укороченный) путь. Если последовательная цепочка работ соединяет исходное и завершающее события сети, то такой путь называется полным. Неполный путь соединяет рассматриваемое событие с исходным или завершающим событием или два любых заданных события сетевого графика. На практике в основном производится анализ и расчет полных путей. Очевидно, ввиду того, что условия и длительность выполнения работ различны, продолжительность полных путей сети имеет разное значение. Сравнение всех полных путей сетевого графика выявляет такой, длительность которого имеет максимальную продолжительность, который называют критическим путем. Все работы критического пути являются потенциальным узким местом, требуют наибольшего внимания при планировании. Работы критического пути выделяют жирными или двойными линиями для наглядного представления той последовательности работ, которая определяет общий срок выполнения всего комплекса работ.
Выделение критического пути является основой оптимизации сетевой модели. Работы, не лежащие на критическом пути, обладают резервом времени, т.е. допустимыми сдвигами сроков их выполнения, не меняющими срока наступления завершающего события или даже сроков выполнения других работ сетевого плана. Наличие запаса времени имеет большое значение, т.к. позволяет маневрировать внутренними ресурсами. По ходу выполнения программы в пределах имеющегося запаса времени можно увеличивать продолжительность некритических работ и переводить освободившихся работников на работы, находящиеся на критическом пути, от которых зависит в данный момент времени выполнение всего комплекса.
Сетевой график можно строить по комбинационной схеме, когда работы ближайшего периода детализируются с большей степенью, а отдаленного периода – с меньшей.
Основной способ изображения сетевого графика – комбинированный, при котором стрелки изображают работы, имеющие наименование, а кружки – события с порядковыми номерами. Смотри график (рис.1).
Второй способ – сеть, ориентированная на событие. События отображаются кружками, но стрелки на таком графике отображают не работы, а этапы и служат лишь для указания последовательности свершения событий во времени. Моделируются в этом случае не процессы выполнения всех работ, а его этапность, последовательность получения результатов. Такие модели концентрируют внимание не на том, какие работы предстоит выполнять, а на том, какие результаты должны быть получены при выполнении этих работ. Эти модели целесообразно применять для укрупненного изображения процесса, когда детальное изображение затруднено или не нужно.
Третий способ – сеть, ориентированная на работы. На этом графике работы изображаются в виде кружков, а стрелки отражают взаимосвязи между работами. Такие сети обычно составляются на начальном этапе и характерны для несложных процессов. Применяются редко.
Приступая к построению сети, необходимо, прежде всего, четко сформулировать работы и определить результаты, которыми они должны завершаться. Для каждой работы следует установить:
- какие работы должны быть завершены раньше, чем начнется данная работа;
- какие работы могут быть начаты после завершения данной работы;
- какие работы могут выполняться одновременно с данной работой.
На основе данного анализа последовательности выполнения и взаимосвязи работ между собой составляется таблица, которая содержит все необходимые исходные данные для построения сетевого графика.
Таблица 1
| № | Код работы | Наименование работы | После каких работ идет данная работа | Какие работы следуют после данной работы | Продолжительность работы | |
| минимальная | максимальная | |||||
При построении сетевого графика следует придерживаться некоторых общих положений:
· сеть вычерчивается слева направо;
· каждое событие с большим порядковым номером изображается правее предыдущего;
· нумерацию событий целесообразно осуществлять после построения сети;
· следует избегать взаимного пересечения стрелок;
· в сети не должно быть событий (кроме завершающего и тупиковых), из которых не выходит ни одной работы;
· в сети не должно быть событий (кроме исходного и «хвостатых»), в которые не входит ни одной работы;
· в сети не должно быть работ и событий, имеющих одинаковые цифры. Если работы выполняются параллельно с одинаковым началом и результатом, то вводится фиктивная работа;
· если какие-либо работы (2-3) в сети могут быть начаты до полного окончания непосредственно предшествующей работы (1-2), то последняя должна быть расчленена на такие последовательности работ (1-2 и 2-4) результаты которых необходимы и достаточны для возможности начать интересующие нас работы (2-3 и 4-5);
· Если для выполнения какой-либо работы необходимо получить результаты не всех входящих в ее начальное событие работ, а только части из них, то для нее нужно ввести в сеть новое начальное событие, которое являлось бы результатом только для указанной части работ, и соединить новое событие фиктивной работой;
· В сети не должно быть путей, соединяющих какое-либо событие с ним же самим, т.е. циклов, замкнутых контуров, если только этот путь не содержит альтернативных событий.
Обычно составляется черновой вариант сети, часто неупорядоченный и неполный. Чтобы уменьшить время вычислений при определении критического пути, Фалкерсон предложил алгоритм нумерации, который работает следующим образом:
А) найти исходное событие сети, в которое не входит ни одна работа. Присвоить ему номер.
Б) вычеркнуть все работы, выходящие из пронумерованного события. При этом появляется по крайней мере одно новое исходное событие, т.е. событие в которое не входит теперь ни одна работа. Присвоить такому событию номер 2.
В) Повторять такой шаг до тех пор, пока не будут пронумерованы все события.
Главным исходным показателем в сети является продолжительность каждой работы. Сети, в которых продолжительность всех работ можно однозначно установить заранее называются детерминированными. Однако сети применяются чаще всего для моделирования новых или постоянно меняющихся процессов и длительность выполнения работы могут оценить только эксперты на основе своего практического опыта. Задача состоит в том, чтобы создать детерминированную сеть, т.е. чтобы создать однозначные оценки продолжительности выполнения всех работ. Для этого первоначально производится экспертная оценка длительности выполнения работы при наиболее благоприятных условиях (tmin), затем – оценка срока выполнения работы при наихудших условиях (tmax). В соответствии с нормальным законом распределения вероятная продолжительность работы принимается равной:
tij = 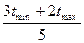 ;
;
Значительно реже продолжительность работы оценивается тремя экспертными показателями:
tij = 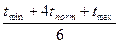 ;
;
После того как определены продолжительности всех работ сетевого графика, можно приступать к расчету остальных временных параметров сети.
При расчете сети, прежде всего необходимо определить возможно более ранний срок достижения цели, который прежде всего зависит от продолжительности критического пути.
Непосредственно на сетевом графике можно рассчитать параметры каждого события: наиболее ранний из возможных сроков его совершения; наиболее поздний срок; резерв времени совершения события. Для этого на графике каждое событие изображается кружком, разделеннои на 4 сектора
Раннее свершение события определяется длительностью критического пути от исходного события к данному событию. Максимально позднее совершения события определяется продолжительностью выполнения всех работ, лежащих на пути к данному событию от исходного события. Поздние сроки совершения всех остальных событий сети определяются исходя из срока совершения завершающего события сети. Поэтому поздний срок совершения любого события равен разности между продолжительностью критического пути и суммарной продолжительностью работ, составляющих максимальный из всех последующих путей, ведущих от данного события к завершающему событию сети.
Для событий критического пути ранние и поздние сроки совершения событий совпадают. События, не лежащие на критическом пути, имеют резерв времени, который показывает, насколько можно задерживать совершение этого события, не влияя на продолжительность критического пути. Он определяется как разница между ранним и поздним сроком наступления события.
К основным параметрам времени, характеризующим отдельную работу, относят:
1) Раннее начало работы. Оно возможно после наиболее раннего окончания всех предшествующих ей работ и определяется ранним сроком совершения начального для работы события.
2) Раннее окончание работы, которое равно сумме раннего начала и продолжительности работы.
3) Позднее окончание работы, которое требуется совершить до самого минимального из всех поздних начал непосредственно последующих за ней работ и определяется поздним сроком совершения конечного для данной работы события.
4) Позднее начало работы равно разности ее позднего окончания и продолжительности.
5)  Полный резерв времени – предельное время, на которое можно увеличить продолжительность данной работы или сместить во времени ее выполнение, не влияя при этом на срок совершения завершающего события, т.е. не изменяя продолжительности критического пути. Полный резерв времени работы определяется резервом времени максимального из путей проходящих через данную работу. Для всех работ критического пути полный резерв времени равен нулю.
Полный резерв времени – предельное время, на которое можно увеличить продолжительность данной работы или сместить во времени ее выполнение, не влияя при этом на срок совершения завершающего события, т.е. не изменяя продолжительности критического пути. Полный резерв времени работы определяется резервом времени максимального из путей проходящих через данную работу. Для всех работ критического пути полный резерв времени равен нулю.
6) Частный (свободный) резерв времени работы – предельное время, на которое можно увеличить продолжительность работы или сместить ее выполнение, не изменяя ранних сроков начала непосредственно следующих за ней работ. Частный резерв времени работы равен разности между ранним сроком совершения ее конечного события и ранним сроком окончания этой работы.
Сроки начала и окончания работ детерминированной сети, а также резервы времени удобно находить табличным способом. В таблице заполняются первые три колонки. После этого находят ранние сроки начала и окончания работ (колонки 4 и 5).
Рассчитав ранние сроки начала и окончания всех работ, выбирают максимальное из полученных ранних окончаний работ, оканчивающихся завершающим событием сети и приравнивают его к позднему окончанию этой работы. Далее рассчитывают колонку7. Поздние окончания предыдущих работ приравнивают к минимальному из поздних начал взаимосвязанных последующих работ и таким образом последовательно снизу вверх в таблице рассматриваются поздние сроки начала и окончания всех работ сети.
После нахождения ранних и поздних сроков начала и окончания всех работ определяют резервы времени каждой работы сети: колонка 8 = колонка 7 – колонка 5 = колонка 6 – колонка 4.
Для определения частного резерва времени сравнивают ее раннее окончание с ранним началом непосредственно следующей за ней работы.
Таблица 2. Определение параметров работы
| Код работы | Срок выполнения работы | Раннее | Позднее | Резервы | ||||||
| № | ij | начало | окончание | начало | окончание | полный | частный | |||
| <== предыдущая страница | | | следующая страница ==> |
| Метод экспертных оценок | | | Применение экономико-математических методов в ППЭ |
Дата добавления: 2014-03-01; просмотров: 337; Нарушение авторских прав

Мы поможем в написании ваших работ!