
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Пусть даны  и
и 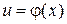 , тогда
, тогда  сложная функция с промежуточным аргументом
сложная функция с промежуточным аргументом 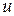 и независимым аргументом
и независимым аргументом  .
.
ТЕОРЕМА: Если функция 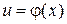 имеет производную
имеет производную  в точке
в точке  , а функция
, а функция  имеет производную
имеет производную  в соответствующей точке
в соответствующей точке 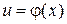 , то сложная функция
, то сложная функция  имеет производную
имеет производную 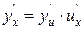 .
.
ДОКАЗАТЕЛЬСТВО: по условию  , отсюда по теореме о связи функции, ее предела и бесконечно малой функции, имеем
, отсюда по теореме о связи функции, ее предела и бесконечно малой функции, имеем
 ;
;
или
 , где
, где 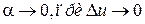
Аналогично получаем для функции 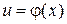 , которая тоже имеет производную в точке
, которая тоже имеет производную в точке  , тогда имеем
, тогда имеем
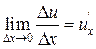 ,
,
следовательно
 или
или 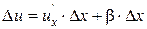 , где
, где 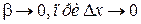
Теперь подставим значение  в
в  , получаем:
, получаем:
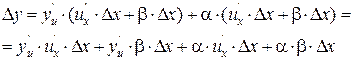
Разделим  на
на  и перейдем к пределу при
и перейдем к пределу при  .
.

Таким образом, получаем 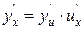 .
.
ИТАК: Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. Это правило остается в силе, если промежуточных аргументов несколько. Так если  ,
,  ,
,  , то
, то  .
.
ПРАКТИЧЕСКИЕ ЗАДАЧИ:
Найти производные функций:
1) 
Функция является сложной, найдем ее производную:

Эту функцию можно представить в виде цепочки «простых» функций:
 , где
, где  ,
,  , где
, где  , по правилу дифференцирования получаем
, по правилу дифференцирования получаем 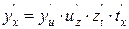
2)  3)
3) 
Пользуясь правилом дифференцирования обратной функции, найти производную 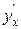 для функции
для функции 
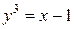 ,
, 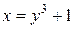 ,
, 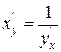 ,
, 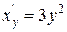 ,
, 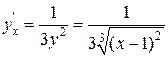
| <== предыдущая страница | | | следующая страница ==> |
| ПРОИЗВОДНАЯ СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ФУНКЦИЙ | | | ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ |
Дата добавления: 2015-07-26; просмотров: 215; Нарушение авторских прав

Мы поможем в написании ваших работ!