Формула Тейлора для функций двух переменных

Теорема 3.6. Если в некоторой d-окрестности точки функция непрерывна и имеет непрерывные частные производные до (n-1)-го порядка включительно, то для любой точки этой окрестности справедлива формула

,

где .

Д о к а з а т е л ь с т в о. Для доказательства используем формулу Маклорена для функции 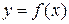одной переменной, которая имеет вид

.

Введем в рассмотрение новую функцию, которая зависит от t

.

Составим для нее формулу Маклорена. Для этого найдем ее производные как сложной функции.

.

.

Далее аналогично можно получить

,

.

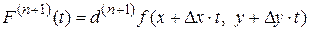Найдем значения функции и ее производных при t = 0:

, ,…, , .

Запишем формулу Маклорена

.

При t = 1 . Формула примет вид

.

Учитывая, что , формулу Маклорена можно записать в виде

.

В частном случае при n = 0 формула принимает вид

или

.

Эта формула является обобщением формулы Лагранжа на случай функции двух переменных.

Дата добавления: 2015-07-26; просмотров: 327; Нарушение авторских прав

Мы поможем в написании ваших работ!