Линейные неоднородные дифференциальные уравнения

Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде: . При этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однороднымдифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднороднымдифференциальным уравнением (P(x) и Q(x) – функции, непрерывные на некотором промежутке a < x < b).

Метод Бернулли. Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций , где u=u(x) и v=v(x) – неизвестные функции от х. Отсюда, .

Подставляя у и 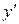в исходное уравнение, получаем:

.

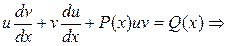
В качестве u берут частное решение уравнения: 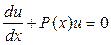. Решая это дифференциальное уравнение, определяем u:

.

Для нахождения второй неизвестной функции v подставим полученное выражение для функции u в исходное уравнение с учетом того, что выражение, стоящее в скобках, равно нулю.

.

Интегрируя, получаем функцию v: .

Подставляя полученные значения u и v в y=uv, получаем:

.

Окончательно получаем формулу: .

Это уравнение является решением неоднородного линейного дифференциального уравнения в общем виде по способу Бернулли.

Метод Лагранжа. Метод Лагранжа решения неоднородных линейных дифференциальных уравнений еще называют методом вариации произвольной постоянной.

Первый шаг: приравниваем правую часть дифференциального уравнения 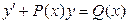к нулю: .

Находится решение получившегося однородного дифференциального уравнения: .

Второй шаг: находим решение неоднородного дифференциального уравнения. Для этого считаем постоянную С₁ некоторой функцией от х. Тогда по правилам дифференцирования произведения функций получаем:

.

Подставляем полученное равенство в исходное уравнение:

.

Упрощаем, преобразуем и получаем: .

Отсюда: .

Подставляя это значение в исходное уравнение: .

Пример. Решить уравнение .

Метод Бернулли. Полагаем и .

Тогда .

1) , , , .

2) , т.е. , .

Итак, .

Метод Лагранжа. Решаем уравнение .

Имеем . Заменяем с на с(х): .

Тогда .

Подставля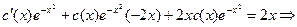ем . Получаем .

Пример. Решить уравнение .

Учитывая, что , то от исходного уравнения переходим к линейному уравнению . Применим подстановку 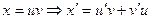. Получаем . Находим .

Находим .

Получаем .

Дата добавления: 2015-07-26; просмотров: 203; Нарушение авторских прав

Мы поможем в написании ваших работ!