
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Санкт-Петербург. §1. Дифференциальные уравнения первого порядка
ПГУПС
§1. Дифференциальные уравнения первого порядка. Основные определения
Дифференциальным уравнением первого порядка называется уравнение вида
 , (1.1)
, (1.1)
где  - независимая переменная,
- независимая переменная,  - неизвестная функция, зависящая от
- неизвестная функция, зависящая от  ,
, 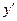 - производная функции
- производная функции  .
.
Определение1.Решением дифференциального уравнения называется непрерывно-дифференцируемая функция  , которая при подстановке в уравнение (1.1) обращает его в тождество.
, которая при подстановке в уравнение (1.1) обращает его в тождество.
На плоскости каждому решению соответствует кривая, которая называется интегральной кривой.
Рассмотрим следующую задачу - найти решение уравнения (1.1), удовлетворяющее условию
 . (1.2)
. (1.2)
Рассмотренная задача называется задачей Коши для уравнения (1.1). Условие (1.2) называется начальным условием .
Определение2. Решение уравнения (1.1), удовлетворяющее начальному условию (1.2), называется решением задачи Коши .
На плоскости решению задачи Коши соответсвует интегральная кривая, проходящая через точку  . Будем рассматривать уравнения, для которых решение задачи Коши существует и единственно.
. Будем рассматривать уравнения, для которых решение задачи Коши существует и единственно.
Определение3. Общим решением уравнения (1.1) называется функция  , зависящая от независимой переменной
, зависящая от независимой переменной  и произвольной постоянной
и произвольной постоянной 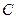 , удовлетворяющая следующим условиям:
, удовлетворяющая следующим условиям:
1) при любом 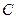 эта функция является решением уравнения (1.1);
эта функция является решением уравнения (1.1);
2)уравнение
 (1.3)
(1.3)
разрешимо относительно 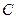 при любых начальных данных
при любых начальных данных  .
.
Определение4.Частным решением уравнения (1.1) называется любое решение,полученное из общего при конкретном выборе произвольной постоянной 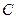 .
.
Если в определениях 1 - 4 функции  заданы неявно , то они называются соответственно интегралом, интегралом задачи Коши, общим интегралом и частным интегралом. Нахождение решений дифференциальных уравнений называется их интегрированием. Для нахождения решения задачи Коши, т.е. решения уравнения (1.1), удовлетворяющего начальному условию (1.2), достаточно построить общее решение уравнения (1.1), найти из условия (1.2)значение постоянной
заданы неявно , то они называются соответственно интегралом, интегралом задачи Коши, общим интегралом и частным интегралом. Нахождение решений дифференциальных уравнений называется их интегрированием. Для нахождения решения задачи Коши, т.е. решения уравнения (1.1), удовлетворяющего начальному условию (1.2), достаточно построить общее решение уравнения (1.1), найти из условия (1.2)значение постоянной 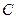 и подставить найденное значение
и подставить найденное значение 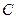 в общее решение.
в общее решение.
Пример1.1. Рассмотрим уравнение 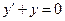 и функции
и функции  ,
,  ,
,  . Определим, какие из функций являются решениями уравнения. Подставляя каждую функцию в исходное уравнение, получим соответственно три соотношения:
. Определим, какие из функций являются решениями уравнения. Подставляя каждую функцию в исходное уравнение, получим соответственно три соотношения:
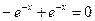 ;
;  ;
;  .
.
Второе соотношение тождеством не является. Следовательно, функция 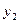 решением не является. Первое соотношение является тождеством, и функция
решением не является. Первое соотношение является тождеством, и функция  зависит только от
зависит только от  и непрерывна вместе с первой производной . Следовательно , функция
и непрерывна вместе с первой производной . Следовательно , функция  является решением. Третье соотношение является тождеством относительно
является решением. Третье соотношение является тождеством относительно  для любого
для любого 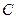 и функция
и функция 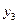 зависит и от переменной
зависит и от переменной  и от произвольной постоянной
и от произвольной постоянной 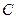 . Проверим выполнение второго условия в определении общего решения. Уравнение (1.3) для функции
. Проверим выполнение второго условия в определении общего решения. Уравнение (1.3) для функции 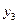 имеет вид
имеет вид  . Отсюда находим , что для любых
. Отсюда находим , что для любых 
 , то есть уравнение (1.3) разрешимо относительно
, то есть уравнение (1.3) разрешимо относительно 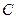 . Таким образом, функция
. Таким образом, функция 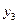 является общим решением.
является общим решением.
§2. Интегрирование основных типов уравнений первого порядка
Рассмотрим уравнение (1.1) предыдущего параграфа. Если из этого уравнения можно выразить 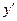 , то оно приводится к виду
, то оно приводится к виду
 (2.1)
(2.1)
и называется уравнением, разрешенным относительно 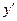 . Заменим
. Заменим 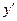 на
на  , а
, а 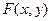 заменим на
заменим на  . Тогда уравнение (2.1) примет вид
. Тогда уравнение (2.1) примет вид  . Перенося правую часть уравнения влево и умножая обе части на
. Перенося правую часть уравнения влево и умножая обе части на 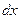 и на
и на  , получим
, получим
 . (2.2)
. (2.2)
Уравнение (2.2) называется уравнением в дифференциальной форме.
10 .Уравнения с разделенными переменными
Уравнением с разделенными переменными называется уравнение вида:
 . (2.3)
. (2.3)
Уравнение (2.3) является уравнением в дифференциальной форме, у которого коэффициент при 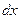 зависит только от
зависит только от  , а коэффициент при
, а коэффициент при  зависит только от
зависит только от  .
.
Общий интеграл уравнения (2.3) имеет вид
 . (2.4)
. (2.4)
20 .Уравнения с разделяющимися переменными
Уравнением с разделяющимися переменными называется уравнение вида:
 . (2.5)
. (2.5)
Уравнение (2.5) является уравнением в дифференциальной форме, причем коэффициенты при 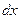 и
и  являются произведением двух функций, одна из которых зависит только от
являются произведением двух функций, одна из которых зависит только от  , а другая - только от
, а другая - только от  . Поделив обе части уравнения (2.5) на
. Поделив обе части уравнения (2.5) на  и
и  , получим уравнение с разделенными переменными
, получим уравнение с разделенными переменными
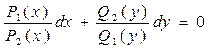 , (2.6)
, (2.6)
общий интеграл которого имеет вид
 . (2.7)
. (2.7)
Пример2.1. Найти общее решение (или общий интеграл) уравнения
 .
.
Это уравнение с разделяющимися переменными. Поделив обе части уравнения на  и на
и на  , получим уравнение с разделенными переменными
, получим уравнение с разделенными переменными
 .
.
Интегрируя , находим общий интеграл уравнения
 .
.
30 .Однородные уравнения первого порядка
Однородным уравнением называется уравнение, которое можно привести к виду:
 . (2.8)
. (2.8)
Уравнение (2.8) является уравнением, разрешенным относительно 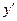 , и аргументом функции
, и аргументом функции  является частное
является частное 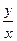 . Однородное уравнение можно привести к уравнению с разделяющимися переменными с помощью стандартной подстановки
. Однородное уравнение можно привести к уравнению с разделяющимися переменными с помощью стандартной подстановки
 (2.9)
(2.9)
или  , (2.10)
, (2.10)
где  - новая неизвестная функция, зависящая от
- новая неизвестная функция, зависящая от  . Подставив
. Подставив  в уравнение (2.8) по формуле (2.9), получим уравнение относительно функции
в уравнение (2.8) по формуле (2.9), получим уравнение относительно функции 
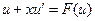 или
или  .
.
Переходя к дифференциальной форме записи уравнения и разделяя переменные ,получим
 .
.
Проинтегрировав полученное уравнение и заменив  на
на 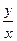 , получим общий интеграл исходного уравнения.
, получим общий интеграл исходного уравнения.
Пример 2.2. Найти решение уравнения
 ,
,
удовлетворяющее начальному условию
 , (2.11)
, (2.11)
то есть найти решение задачи Коши . Сначала найдем общее решение . Уравнение можно записать в виде
 .
.
Уравнение является однородным. Применяя подстановку (2.9), получим уравнение
 или
или  .
.
Переходя к дифференциальной форме, разделяя переменные и интегрируя, получим
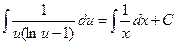 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Дифференциальные уравнения. 1. ДУ с разделяющимися переменными: или | | | Вычислив интегралы, находим |
Дата добавления: 2015-07-26; просмотров: 190; Нарушение авторских прав

Мы поможем в написании ваших работ!