
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Для того чтобы уравнение (2.20) являлось уравнением в полных дифференциалах, необходимо и достаточно выполнение условия
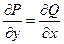 . (2.23)
. (2.23)
Если условие (2.23) выполняется, то функцию 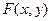 можно определить из условий (2.21). Интегрируя первое соотношение (2.21) по переменной
можно определить из условий (2.21). Интегрируя первое соотношение (2.21) по переменной  , находим
, находим
 . (2.24)
. (2.24)
где  - неизвестная функция , зависящая от
- неизвестная функция , зависящая от  . Уравнение для нахождения
. Уравнение для нахождения  получается при подстановке
получается при подстановке 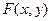 по формуле (2.24) во второе условие (2.21).
по формуле (2.24) во второе условие (2.21).
Пример 2.4 Найти решение уравнения
 ,
,
удовлетворяющее начальному условию  .
. 
Сначала найдем общее решение уравнения.
 ;
;  .
.
Найдем частные производные
 ;
;  .
.
Таким образом, условие (2.23) выполняется, и уравнение является уравнением в полных дифференциалах. Запишем условия (2.21)
 и
и  .
.
Тогда интегрируя по  первое соотношение (при этом
первое соотношение (при этом  играет роль константы), находим
играет роль константы), находим
 .
.
Дифференцируя последнее выражение по  , получим
, получим
 .
.
С другой стороны, из второго условия (2.21)
 .
.
Приравнивая правые части полученных равенств, находим уравнение для определения 
 или
или  .
.
Тогда  . Полагая
. Полагая 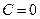 и подставляя
и подставляя  в выражение для функции
в выражение для функции 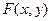 , находим
, находим
 .
.
Общий интеграл имеет вид
 .
.
Подставляя в последнее уравнение из начального условия  и
и 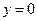 , находим, что
, находим, что  . Тогда решение уравнения ,удовлетворяющее начальному условию, имеет вид
. Тогда решение уравнения ,удовлетворяющее начальному условию, имеет вид
 .
.
§3. Дифференциальные уравнения высших порядков. Основные определения
Дифференциальным уравнением n-го порядка называется выражение вида
 , (3.1)
, (3.1)
где  независимая переменная,
независимая переменная,  - неизвестная функция, зависящая от
- неизвестная функция, зависящая от  ,
,  - производные функции
- производные функции  до
до  -го порядка включительно. Порядком дифференциального уравнения называется порядок старшей производной.
-го порядка включительно. Порядком дифференциального уравнения называется порядок старшей производной.
Основные определения для уравнений высших порядков рассмотрим на примере уравнений второго порядка.
Уравнение второго порядка имеет вид
 . (3.2)
. (3.2)
Определение1.Решением дифференциального уравнения (3.2) называется дважды непрерывно-дифференцируемая функция  , которая при подстановке в уравнение (3.2) обращает его в тождество.
, которая при подстановке в уравнение (3.2) обращает его в тождество.
Рассмотрим следующую задачу - найти решение уравнения (3.2), удовлетворяющее условиям:
 и
и  . (3.3)
. (3.3)
Рассмотренная задача называется задачей Коши для уравнения (3.2). Условия (3.3) называются начальными условиями .
Определение2. Решение уравнения (3.2), удовлетворяющее начальным условиям (3.3), называется решением задачи Коши.
Определение3. Общим решением уравнения (3.2) называется функция  , зависящая от независимой переменной
, зависящая от независимой переменной  и двух произвольных постоянных
и двух произвольных постоянных  и
и  , удовлетворяющая следующим условиям:
, удовлетворяющая следующим условиям:
1) при любых  и
и  эта функция является решением уравнения (3.2);
эта функция является решением уравнения (3.2);
2)уравнения
 и
и  (3.4)
(3.4)
разрешимы относительно  и
и  при любых начальных данных
при любых начальных данных 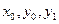 .
.
Определение4.Частным решением уравнения (3.2) называется любое решение,полученное из общего при конкретном выборе произвольных постоянных  и
и  .
.
§4.Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
 , (4.1)
, (4.1)
где 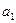 и
и  - заданные числа, а
- заданные числа, а  - заданная функция .
- заданная функция .
Если 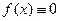 , то есть
, то есть
 , (4.2)
, (4.2)
то уравнение называется линейным однородным. В противном случае, то есть если  , уравнение называется линейным неоднородным. Введем следующие обозначения:
, уравнение называется линейным неоднородным. Введем следующие обозначения:
 - общее решение неоднородного уравнения (4.1),
- общее решение неоднородного уравнения (4.1),
 - общее решение однородного уравнения (4.2),
- общее решение однородного уравнения (4.2),
 - какое-либо частное решение неоднородного уравнения (4.1).
- какое-либо частное решение неоднородного уравнения (4.1).
Тогда справедлива теорема о структуре общего решения линейного неоднородного уравнения:
 . (4.3)
. (4.3)
10. Построение общего решения линейного однородного уравнения
Рассмотрим однородное уравнение (4.2). Справедлива теорема о структуре общего решения линейного однородного уравнения :
 , (4.4)
, (4.4)
где  и
и  - любые линейно независимые решения однородного уравнения.
- любые линейно независимые решения однородного уравнения.
Характеристическим уравнением для уравнения (4.2)будем называть следующее алгебраическое уравнение:
 . (4.5)
. (4.5)
Его коэффициенты совпадают с коэффициентами при  в уравнении (4.2).
в уравнении (4.2).
Уравнение (4.5) является квадратным уравнением относительно  и имеет два корня (с учетом кратных и комплексных). Обозначим его корни через
и имеет два корня (с учетом кратных и комплексных). Обозначим его корни через  и
и  .
.
Вид функций  и
и  , входящих в общее решение, зависит от типа корней характеристического уравнения. Возможны следующие случаи:
, входящих в общее решение, зависит от типа корней характеристического уравнения. Возможны следующие случаи:
1.  и
и  вещественны и различны, то есть
вещественны и различны, то есть  ,
,
2.  и
и  вещественны и равны, то есть
вещественны и равны, то есть  ,
,
3.  и
и  - комплексные корни
- комплексные корни  , где
, где  - вещественная часть, а
- вещественная часть, а  - мнимая часть комплексного числа.
- мнимая часть комплексного числа.
Общее решение для каждого случая соответственно имеет вид:
1.  ,
,
2.  ,
,
3. 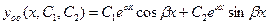 .
.
Пример 4.1. Найти общее решение уравнения
 .
.
Характеристическое уравнение имеет вид  . Отсюда находим
. Отсюда находим  ,
,  . Найденные корни вещественны и различны (случай 1). Тогда получим
. Найденные корни вещественны и различны (случай 1). Тогда получим  .
.
Пример 4.2 Найти общее решение уравнения
 .
.
Характеристическое уравнение имеет вид  . Отсюда находим
. Отсюда находим  (случай 2). Тогда общее решение имеет вид
(случай 2). Тогда общее решение имеет вид  .
.
. Пример 4.3 Найти общее решение уравнения
 .
.
Характеристическое уравнение имеет вид  . Отсюда находим
. Отсюда находим  . Корни комплексные.
. Корни комплексные.  ,
,  (случай 3). Общее решение имеет вид
(случай 3). Общее решение имеет вид  .
.
20. Построение частного решения линейного неоднородного уравнения методом неопределенных коэффициентов
Для некоторых видов неоднородных уравнений (4.1) по виду правых частей  можно определить вид частного решения
можно определить вид частного решения  с точностью до неизвестных коэффициентов, а затем , подставив частное решение в уравнение (4.1), получить систему для нахождения этих коэффициентов.
с точностью до неизвестных коэффициентов, а затем , подставив частное решение в уравнение (4.1), получить систему для нахождения этих коэффициентов.
Рассмотрим стандартные виды правых частей  и соответствующие им виды частных решений:
и соответствующие им виды частных решений:
1.  , то есть
, то есть  - многочлен степени n.
- многочлен степени n.
1.а. Если число  не является корнем характеристического уравнения (4.5), то частное решение уравнения (4.1) ищется в виде
не является корнем характеристического уравнения (4.5), то частное решение уравнения (4.1) ищется в виде
 ,
,
где  - неизвестные коэффициенты.
- неизвестные коэффициенты.
1.b Если число  является корнем характеристического уравнения (4.5) кратности
является корнем характеристического уравнения (4.5) кратности  (
(  может принимать значения 1 или 2), то частное решение уравнения (4.1) ищется в виде
может принимать значения 1 или 2), то частное решение уравнения (4.1) ищется в виде
 .
.
2.  , то есть
, то есть  - произведение
- произведение  на многочлен.
на многочлен.
2.a Если число  (коэффициент при
(коэффициент при  в показателе степени у
в показателе степени у  ) ,
) ,
не является корнем характеристического уравнения (4.5), то частное решение уравнения (4.1) ищется в виде
 .
.
2.b Если число  является корнем характеристического уравнения (4.5) кратности
является корнем характеристического уравнения (4.5) кратности  (
(  может принимать значения 1 или 2), то частное решение уравнения (4.1) ищется в виде
может принимать значения 1 или 2), то частное решение уравнения (4.1) ищется в виде
 .
.
3.  .
.
3.a Если число  (
(  -коэффициент при
-коэффициент при  в показателе степени у
в показателе степени у  ,
,  -коэффициент при
-коэффициент при  у синуса и косинуса) ,
у синуса и косинуса) ,
не является корнем характеристического уравнения (4.5), то частное решение уравнения (4.1) ищется в виде
 ,где
,где 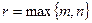 .
.
3.b Если число  является корнем характеристического уравнения (4.5) (кратность этого корня может быть равной только 1 , так как характеристическое уравнение второй степени ), то частное решение уравнения (4.1) ищется в виде
является корнем характеристического уравнения (4.5) (кратность этого корня может быть равной только 1 , так как характеристическое уравнение второй степени ), то частное решение уравнения (4.1) ищется в виде

Пример 4.4 Найти решение уравнения  ,
,
удовлетворяющее начальным условиям  ,
,  .
.
Характеристическое уравнение имеет вид  .Отсюда находим
.Отсюда находим  ,
,  . Тогда общее решение однородного имеет вид
. Тогда общее решение однородного имеет вид  . Правая часть исходного уравнения является многочленом второй степени. При этом
. Правая часть исходного уравнения является многочленом второй степени. При этом  не является корнем характеристического многочлена (случай 1.a). Поэтому частное решение неоднородного уравнения ищем в виде
не является корнем характеристического многочлена (случай 1.a). Поэтому частное решение неоднородного уравнения ищем в виде
 .
.
Находим производные.  ,
,  .
.
Подставляя  в исходное уравнение, получим
в исходное уравнение, получим
 .
.
Приравнивая коэффициенты при одинаковых степенях  в левой и правой частях равенства, находим систему для определения
в левой и правой частях равенства, находим систему для определения 
 .
.
Отсюда  ,
,  ,
,  . Тогда
. Тогда  . Используя формулу (4.3), получим общее решение неоднородного уравнения
. Используя формулу (4.3), получим общее решение неоднородного уравнения
 .
.
Найдем решение задачи Коши .
 .
.
Удовлетворяя начальным условиям, получим систему для определения  и
и 
 .
.
Отсюда  ;
;  . Подставив найденные
. Подставив найденные  и
и 
в общее решение, окончательно получим решение задачи Коши
 .
.
Пример 4.5 Найти решение уравнения  ,
,
удовлетворяющее начальным условиям  ,
,  .
.
Характеристическое уравнение имеет вид  .Отсюда находим
.Отсюда находим  ,
,  . Тогда общее решение однородного имеет вид
. Тогда общее решение однородного имеет вид  . Правая часть исходного уравнения является произведением многочлена первой степени на
. Правая часть исходного уравнения является произведением многочлена первой степени на 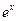 .При этом
.При этом  является корнем характеристического многочлена кратности
является корнем характеристического многочлена кратности  (случай 2.b). Поэтому частное решение неоднородного уравнения ищем в виде
(случай 2.b). Поэтому частное решение неоднородного уравнения ищем в виде
 .
.
Находим производные.
 ,
,
 .
.
Подставляя  в исходное уравнение и выполнив элементарные преобразования, получим
в исходное уравнение и выполнив элементарные преобразования, получим
 .
.
Поделив обе части уравнения на 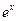 и приравнивая коэффициенты при одинаковых степенях
и приравнивая коэффициенты при одинаковых степенях  в левой и правой частях равенства, находим систему для определения
в левой и правой частях равенства, находим систему для определения  и
и 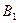
 .
.
Отсюда  ,
,  . Тогда
. Тогда  . Используя формулу (4.3), получим общее решение неоднородного уравнения
. Используя формулу (4.3), получим общее решение неоднородного уравнения
 .
.
Найдем решение задачи Коши .
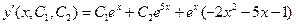 .
.
Удовлетворяя начальным условиям, получим систему для определения  и
и 
 .
.
Отсюда  ,
,  . Подставив найденные С1 и С2 в общее решение, окончательно получим решение задачи Коши
. Подставив найденные С1 и С2 в общее решение, окончательно получим решение задачи Коши
 .
.
§5. Построение решения задачи Коши линейных дифференциальных уравнений второго порядка с постоянными коэффициентами операционным методом
При построении решения задачи Коши операционным методом используют преобразование Лапласа [1], которое функции  вещественной переменной
вещественной переменной  по определенному правилу ставит в соответствие функцию
по определенному правилу ставит в соответствие функцию  комплексной переменной
комплексной переменной  . Функция
. Функция  называется оригиналом , а функция
называется оригиналом , а функция  - изображением. При этом используется следующее обозначение:
- изображением. При этом используется следующее обозначение:
 . (5.1)
. (5.1)
Последняя запись означает, что функция  имеет изображение
имеет изображение  . Составлены специальные таблицы оригиналов и изображений [1].
. Составлены специальные таблицы оригиналов и изображений [1].
Справедливо свойство линейности изображения: если  и
и  , то для любых чисел
, то для любых чисел 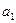 и
и 
 .
.
Рассмотрим линейное дифференциальное уравнение
 (5.2)
(5.2)
и начальные условия
 и
и  . (5.3)
. (5.3)
Обозначим через  решение уравнения (5.2), удовлетворяющее начальным условиям (5.3), а через
решение уравнения (5.2), удовлетворяющее начальным условиям (5.3), а через  - его изображение.
- его изображение.
Справедливы следующие формулы для изображений производных функции  :
:
 ,
,  . (5.4)
. (5.4)
Преобразование Лапласа переводит дифференциальное уравнение в следующее уравнение:
 (5.5)
(5.5)
В уравнении (5.5)  - изображение
- изображение  ;
;  - изображение функции
- изображение функции  , которое определяется по таблице оригиналов и изображений. Уравнение (5.5) является алгебраическим уравнением относительно
, которое определяется по таблице оригиналов и изображений. Уравнение (5.5) является алгебраическим уравнением относительно  . Из этого уравнения определяют
. Из этого уравнения определяют  как функцию, зависящую от
как функцию, зависящую от  , а затем по таблице оригиналов и изображений находят искомое решение задачи Коши
, а затем по таблице оригиналов и изображений находят искомое решение задачи Коши  .
.
| <== предыдущая страница | | | следующая страница ==> |
| Тогда уравнение (2.16) примет вид | | | Пример5.1 |
Дата добавления: 2015-07-26; просмотров: 275; Нарушение авторских прав

Мы поможем в написании ваших работ!