Пример5.1

Найти решение уравнения ,удовлетворяющее условиям , .

Тогда , ,

, , . .

По таблице изображений находим 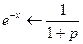. Уравнение в изображениях (5.5) примет вид

Отсюда находим

Используя таблицу оригиналов и изображений, окончательно получим решение задачи Коши

.

Приложение 1.

Таблица оригиналов и изображений.

1.		6.
2.		7.
3.		8.
4.		9.
5.		10.

§6.Нахождение решения задачи Коши приближенным методом Эйлера (на примере уравнения первого порядка)

Рассмотрим уравнение первого порядка в нормальной форме

(6.1)

и начальное условие

. (6.2)

Обозначим через решение уравнения (6.1), удовлетворяющее условию (6.2), то есть решение задачи Коши. Будем предполагать, что существует и единственно.

В методе Эйлера функция строится приближенно в точках . Пусть - промежуток изменения переменной . Разобъем его на равных частей точками .

,

где .

Значение функции в точке известно и из условия (6.2) равно . Обозначим , , ¼ , .

Справедливы следующие приближенные формулы - формулы Эйлера

,

,

¼ ¼ ¼ ¼ ¼ ¼

(6.3) .

§7. Пример выполнения контрольной работы

Задача1. Найти общее решение (общий интеграл) уравнения

.

Решение.Уравнение записано в дифференциальной форме и после элементарных преобразований приводится к виду

.

Сравнивая полученное уравнение с (2.5), убеждаемся, что задача1 – уравнение с разделяющимися переменными. (§2,пункт 2). Разделяя переменные, имеем

.

Дата добавления: 2015-07-26; просмотров: 200; Нарушение авторских прав

Мы поможем в написании ваших работ!