Дифференциальные уравнения с разделяющимися переменными. Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида

Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида:

,

,

,

,

.

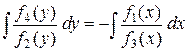Замечание. Проделанные выше преобразования очевидно равносильно только в том случае, когда .

Пример 1. Проинтегрировать дифференциальное уравнение:

.

Решение: Данное уравнение является дифференциальным уравнением с разделяющимися переменными.

,

,

,

, где ,

.

Семейство интегральных кривых представляет семейство концентрических окружностей с центром в точке включая сам центр.

Найдем частное решение уравнения, удовлетворяющее начальному условию :

.

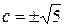
Ответ: , − частное решение, удовлетворяющее начальному условию .

Пример 2. Проинтегрировать дифференциальное уравнение:

.

Решение: ,

,

,

,

,

,

.

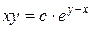Ответ: .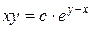

Пример 3. Найти общий интеграл дифференциального уравнения:

.

Решение: Полагая , запишем данное уравнение в виде

или .

Разделим это уравнение на : .

Интегрируя, получаем:

,

,

.

Это есть общий интеграл дифференциального уравнения.

Ответ: .

Пример 3. Решить задачу Коши: , .

Решение: Разделяя переменные и интегрируя, получаем:

,

,

, .

Потенцируя, находим общий интеграл:

.

Подставляя в последнее равенство начальные условия и , получаем . Тогда частное решение примет вид:

,

откуда

.

Это есть частное решение исходного дифференциального уравнения, удовлетворяющего начальному условию .

Ответ: − частное решение уравнения, удовлетворяющего начальному условию .

Дата добавления: 2015-07-26; просмотров: 199; Нарушение авторских прав

Мы поможем в написании ваших работ!