Линейные уравнения первого порядка. Уравнение Я. Бернулли

Определение. Линейным уравнением первого порядка называется уравнение вида: где и функции непрерывные на одном и том же промежутке.

К решению данного уравнения приводит следующая постановка (метод И. Бернулли):

, ,

,

.

Так как функция представлена в виде произведения двух вспомогательных функций, то одну из них мы можем выбирать по своему усмотрению, а именно выберем функцию так, чтобы содержимое квадратной скобки обратилось в ноль.

,

,

,

,

,

,

,

,

,

,

,

.

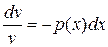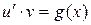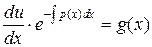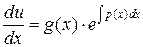Итак, .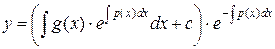

Пример 1. Решить задачу Коши: , .

Решение: Данное уравнение линейно относительно и 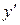. Следовательно, оно есть линейное дифференциальное уравнение первого порядка. Произведем в нем подстановку: , .

Тогда получаем:

,

.

Выберем функцию так, чтобы

,

,

,

,

,

,

,

.

При таком выборе функции уравнение примет вид:

,

,

,

,

,

.

Таким образом, решение данного дифференциального уравнения имеет вид:

.

Используя начальное условие, находим . Подставляя значение в последнее равенство, получим искомое частное решение:

.

Итак, − частное решение данного дифференциального уравнения, удовлетворяющее начальному условию .

Ответ: − частное решение уравнения, удовлетворяющее начальному условию .

Пример 2. Найти общее решение дифференциального уравнения:

.

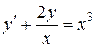Решение: Данное уравнение линейно относительно и 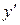. Следовательно, оно есть линейное дифференциальное уравнение первого порядка. Произведем в нем подстановку: , .

Тогда получим:

,

,

,

,

,

,

,

.

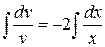При таком выборе функции уравнение примет вид:

,

,

,

.

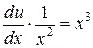Таким образом, решение данного дифференциального уравнения имеет вид:

.

Ответ: .

Пример 3. Найти общее решение дифференциального уравнения:

.

Решение: Данное уравнение не является для функции линейным, но оно линейное относительно функции . Умножим обе части уравнения на .

,

,

,

, ,

,

,

,

,

,

,

.

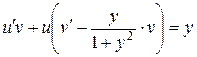При таком выборе функции уравнение примет вид:

,

,

,

.

Таким образом, решение данного дифференциального уравнения имеет вид:

,

.

Ответ: − общее решение дифференциального уравнения.

Определение. Уравнение вида

, ,

(1)

называется уравнением Бернулли.

Покажем, что его можно привести к линейному.

Если , то уравнение (1) − линейное, а при − с разделяющимися переменными.

В общем случае, разделив уравнение (1) на , получим:

.

(2)

Обозначим . Тогда . Отсюда находим . Уравнение (2) примет вид

.

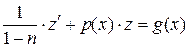Последнее уравнение является линейным относительно . Решение его известно. Таким образом, подстановка сводит уравнение (1) к линейному. На практике дифференциальное уравнение (1) удобнее решать методом И. Бернулли в виде (не сводя его к линейному).

Пример 4. Найти общее решение дифференциального уравнения .

Решение: Данное уравнение является уравнением Я. Бернулли. Применяя подставку , получим:

.

,

,

.

Найдем решение последнего уравнения:

.

Тогда исходное уравнение примет вид:

,

,

,

,

.

Общим уравнением данного дифференциального уравнения будет:

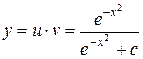или .

Ответ: .

Дата добавления: 2015-07-26; просмотров: 214; Нарушение авторских прав

Мы поможем в написании ваших работ!