Уравнение в полных дифференциалах. называется уравнением в полных дифференциалах, если Р(x,y) и Q(x,y) – непрерывные, дифференцируемые функции

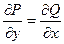(2)

Интегрирование уравнений в полных дифференциалах. Докажем, что если левая часть уравнения (1) есть полный дифференциал некоторой функции u(x, y), то выполняется условие (2), и обратно – при выполнении условий (2) левая часть уравнения (1) есть полный дифференциал некоторой функции u(x, y), т.е. уравнение (1) имеет вид

du(x, y) = 0.

Общий интеграл тогда u(x, y) = C.

Необходимость. Пусть левая часть (1) есть полный дифференциал некоторой функции u(x, y), т.е.

Тогда

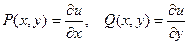
(3)

Отсюда

Следовательно,

,

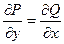т.е. равенство (2) является необходимым условием того, чтобы левая часть уравнения (1) была полным дифференциалом некоторой функции u(x, y). Покажем, что это условие является и достаточным, т.е. покажем, что существует функция u(x, y), полный дифференциал которой равен левой части уравнения (1).

Из первого соотношения (3) находим

(4)

где x₀ – абсцисса любой точки из области существования решения. При интегрировании по x мы считали y постоянным, поэтому произвольная постоянная может зависеть от y. Подберем функцию φ(x) так, чтобы выполнялось второе соотношение (3). Для этого дифференцируем обе части равенства (4) по y и результат приравниваем к Q(x, y).

При этом использовалась формула Лейбница дифференцирования по параметру y. Исходя из соотношении (2), имеем

Следовательно,

Общий интеграл имеет вид

= С

П р и м е р .

Следовательно, данное уравнение есть уравнение в полных дифференциалах. Тогда

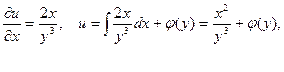
Дифференцируя по y, получим

Общий интеграл исходного уравнения есть

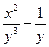=С