Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
Вычисления производных некоторых элементарных функций
1. y=c (c= const) Dy=c-cÞ 
. Итак, 
.
Замечание 1. Производная произведения функции на постоянную равна произведению этой постоянной на производную функции, т.е.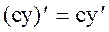 
.
Доказательство.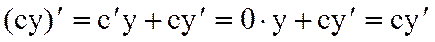 
.
Замечание 2.Если n - любое фиксированное целое число, то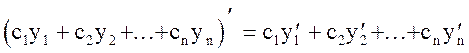 
.
Следует из предыдущей теоремы с помощью метода математической индукции.
2. y=xn (степенная функция), где n - положительное целое число.
Если использовать формулу бинома Ньютона, получим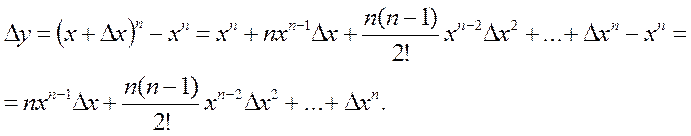 
При Dx¹0
При Dx®0 все слагаемые правой части, начиная со второго, стремятся к нулю, т.к. содержат Dx в некоторой положительной степени. Первое слагаемое Dx не содержит, поэтому предел правой части при Dx®0 равен nxn-1. Следовательно, существует предел левой части при Dx®0, равный nxn-1. По определению производной указанный предел равен производной функции y=xn, т.е.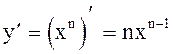 
.
Данные рассуждения справедливы для любой точки xÎ(-¥, +¥).
Кроме того, эту формулу можно обобщить на тот случай, когда n является произвольным вещественным числом (доказательство этого положения см. в п. 4.6.).
3. y=sinx.
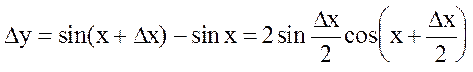. При Dx¹0
. (1)
В силу непрерывности функции cosx в любой точке xÎ(-¥, +¥) 
1 . Если учесть также, что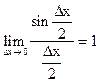 
(см. п.3.16), получим, что предел правой части равенства (1) существует и равен cosx (на основании теоремы 1 п.3.10), а тогда и предел левой части этого равенства существует и равен cosx. По определению производной указанный предел равен производной функции y=sinx, т.е. 
.
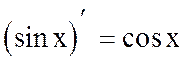4. Аналогичным образом можно показать, что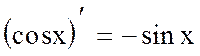 
.
5. 
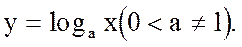Пусть xÎ(0,¥), и Dx - произвольное приращение аргумента, такое что êDx ê<x.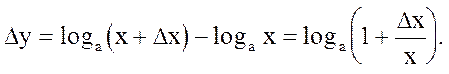 
При Dx¹0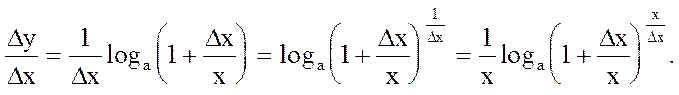 
Если x - фиксировано, то при 
и на основании непрерывности функции 
в любой точке полупрямой (0,¥) и, в частности, в точке 
получим, что 
Поэтому существует предел правой части равенства при 
Но по определению, 
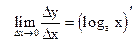, поэтому 
В частности, при а=е
имеем 
6. y=tgx, 
(см. теорему 1 п.3.10)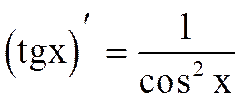 
.
7. y=ctgx. Аналогично этому 
Прежде, чем вычислять производные других элементарных функций, докажем теорему о производной обратной функции.
| <== предыдущая страница | | | следующая страница ==> |
| Доказательство. Так как функция дифференцируема в точке x, Dy=ADx+aDx | | | Теорема. 1) определена, непрерывна и строго монотонна в некоторой окрестности точки x0 |
Дата добавления: 2015-07-26; просмотров: 206; Нарушение авторских прав
Мы поможем в написании ваших работ!