Возрастание (убывание) функций в точке. Локальный экстремум

1. Рассмотрим функцию y=f(x), определенную в некоторой окрестности U(c) точки с.

Определение 1.Функция f(x) называется возрастающей в точке С, если существует d - окрестность точки c(U_d(c)) такая, что

.

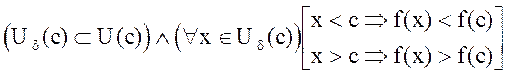Определение 2.Функция f(x) называется убывающей в точке С, если существует d - окрестность точки c(U_d(c)) такая, что

.

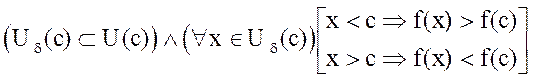Определение 3.Точка с называется точкой локального максимума (локального минимума) функции f(x) (f(x) имеет локальный минимум в точке С), если существует такая d - окрестность точки c(U_d(c)) такая, что

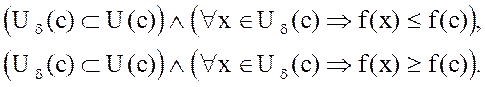
Определение 4.Будем говорить, что функция y=f(x) имеет в точке С локальный экстремум, если эта функция имеет в точке С либо локальный максимум, либо локальный минимум (рис.1)

Рис. 1

Функция f(x) имеет в точке с₁ локальный максимум, в точке с₂ - локальный минимум. Заметим, что f(с₁)<f(с₂).

Теорема 1.(лемма Ферма) (достаточное условие возрастания (убывания) функции в точке). Пусть функция f(x) дифференцируема в точке с и , тогда y=f(x) возрастает (убывает) в точке С.

Замечание 1.Положительность (отрицательность) производной 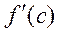не является необходимым условием возрастания (убывания) дифференцируемой в точке С функции y=f(x).

Пример 1.(рис.2). f(x)=x³ возрастает в точке х = 0, но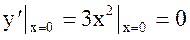

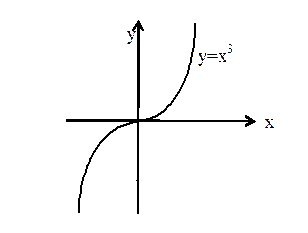рис. 2

Теорема 2.(необходимое условие экстремума дифференцируемой в данной точке функции) (теорема Ферма).

Пусть функция f(x) дифференцируема в точке С и имеет в этой точке локальный экстремум, тогда (рис. 3).

Доказательство.По условию теоремы существует . Так как функция y=f(x) имеет в точке С локальный экстремум, она не может в этой точке ни возрастать, ни убывать. Следовательно, по теореме 1 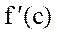не может быть ни положительной ни отрицательной, т.е. .

Теорема доказана.

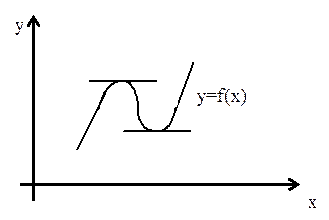
Рис. 3

Замечание 2.Как показано на рис. 3 касательная к графику дифференцируемой функции в точке экстремума горизонтальна.

Пример 2.y=x³, 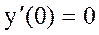, но функция не имеет экстремума, т.е. необходимое условие (теорема 2) экстремума не является достаточным.

Дата добавления: 2015-07-26; просмотров: 235; Нарушение авторских прав

Мы поможем в написании ваших работ!