Теорема о нуле производной

Теорема(теорема Ролля).

Пусть функция f(x) непрерывна на сегменте и дифференцируема во всех внутренних точках этого сегмента, а значения функции на концах сегмента одинаковы, тогда внутри сегмента найдется такая точка, в которой значение производной обращается в нуль.

.

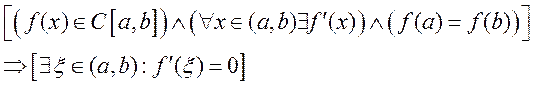Доказательство.f(x)Î C[a,b] (по второй теореме Вейерштрасса) f(x) достигает на [a,b] своих точных верхней и нижней граней (M и m соответственно). Могут представиться два случая:

1) M=m; 2) M>m. Рассмотрим оба этих случая.

1) M=mÞf(x)=M=m=constÞ 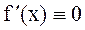"x Î [a,b].

2) M>m. Так как f(a)=f(b), хотя бы одно из двух значений M и m достигается во внутренней точке x сегмента [a,b]. Но тогда функция f(x) имеет в точке x локальный экстремум. По необходимому условию экстремума (теорема Ферма см. п.5.1) =0. Теорема доказана.

Замечание 3.Кратко можно сказать, что между двумя равными значениями дифференцируемой функции обязательно лежит нуль производной, то есть существует хотя бы одна точка, в которой касательная к графику функции горизонтальна (рис.1).

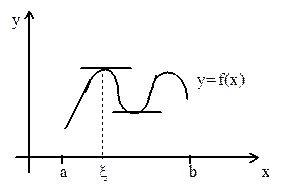
Рис. 1

Приведем несколько примеров, когда при нарушении хотя бы одного из условий теоремы утверждение теоремы не имеет места.

а) Функция f(x)=x-E(x) (E(x) - целая часть от x) на сегменте [0,1] не является непрерывной (рис.2). И хотя все остальные условия теоремы выполнены, однако на (0,1) не существует точки x такой, чтобы 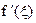=0.

Рис. 2

б) Нарушено условие дифференцируемости на (а, b)

Рис. 3

в) Нарушено условие f(a)=f(b).

Для функции f(x)=x на [0, 1] (рис.4) нет точки xÎ(0, 1), в которой значение производной обращалось бы в 0.

Рис. 4

1.5.14.3. Формула конечных приращений (теорема Лагранжа)

Теорема. Если функция определена и непрерывна на [a,b] и дифференцируема на (a,b), то внутри сегмента [a,b] найдется точка x такая, что справедлива формула

f(b)-f(a)= 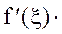(b-a).

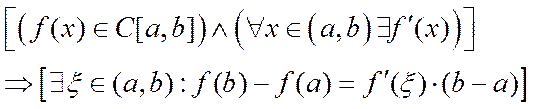
(Формула f(b)-f(a)= (b-a) называется формулой Лагранжа или формулой конечных приращений).

Доказательство.Рассмотрим на сегменте [a,b] вспомогательную функцию (рис.1)

.

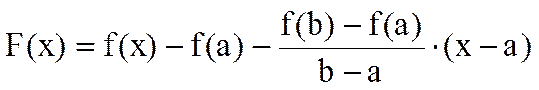Проверим, что для функции F(x) выполнены все условия теоремы Ролля.

1) F(x)ÎC[a,b] (как разность f(x) и линейной функции);

2) $ ;

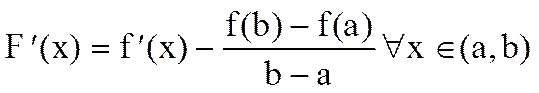3) F(a)=F(b)=0.

По теореме Ролля 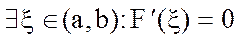, т.е.

.

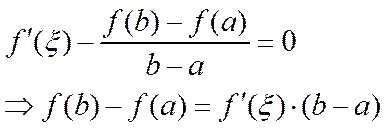Теорема доказана.

Рис. 1

Замечание 1.Напишем уравнение прямой l, проходящей через точки A(a, f(a)) и B(b,f(b)).

.

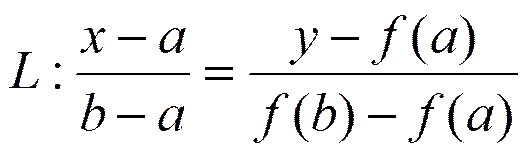Отсюда

.

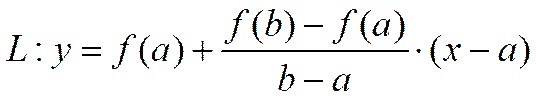Вычитая эту функцию из f(x), получим F(x), для которой F(a)=F(b)=0.

Угловой коэффициент построенной прямой l равен 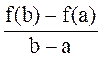. Теорема Лагранжа утверждает, что найдется такая точка xÎ(a,b), в которой угловой коэффициент касательной 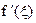совпадает с угловым коэффициентом прямой l, т.е. касательная к графику функции в точке С(x,f(x)) параллельна прямой l, проходящей через точки A и В.

Замечание 2.Другой вид формулы Лагранжа.

Пусть х₀ -любое значение аргумента из [a,b], а Dх- произвольное приращение аргумента, но такое, что 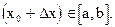Тогда формула Лагранжа для сегмента [x₀ ,x₀+ Dх] имеет следующий вид: ,

,

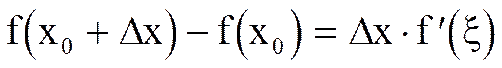где x- некоторая точка из интервала

(x₀ ,x₀+ Dх) (см. рис.2).

Рис. 2

Можно утверждать, что найдется такое число q (0<q<1), зависящее от Dх, что

x= x₀+ qDх, тогда ,

где q некоторое число: 0<q<1.

Этот вид формулы оправдывает термин “формула конечных приращений”, ибо дается выражение для приращения функции через вызвавшее его произвольное конечное приращение Dх аргумента.

Дата добавления: 2015-07-26; просмотров: 247; Нарушение авторских прав

Мы поможем в написании ваших работ!