Соответствия, отображения, функции. Взаимнооднозначные соответствия и мощности множеств. Теорема Кантора. Элементы теории нечетких множеств (2 час)

Цель работы: Ознакомиться с взаимнооднозначными соответствиями и мощности множеств. Рассмотреть Теорему Кантора. Элементы теории нечетких множеств

Порядок выполнения работы:

Практическая работа рассчитана на 2 часа аудиторных занятий, включающих в себя следующее:

1. Изучить:

- Взаимнооднозначные соответствия и мощности множеств.

- Счетные множества, теоремы о счетных множествах.

- Множества мощности континуума. Теорема Кантора.

- Способы задания нечетких множеств.

- Операции над нечеткими множествами.

2. Решить упражнения к разделу «Нечеткие множества». Выполнить каждый пункт упражнения согласно варианту. Вариант определяется как сумма двух последних цифр зачётной книжки, если количество заданий в пункте упражнения меньше, чем полученная цифра, то эта цифра делится пополам (берётся её целая часть).

3. Оформить отчет о проделанной работе в соответствии с требованиями.

4. Проработать контрольные задания СРС.

Требования к отчету:

Отчет по практической работе распечатывается в виде твердой копии и состоит из следующих пунктов:

Вариант индивидуального задания;

Результаты полученных решений заданий;

Ответы на контрольные задания СРС.

Методические указания

Отношения соответствия.

В общем случае между элементами множеств А и В могут быть четыре вида соответствия в зависимости от того, один или несколько элементов множества А соответствуют элементу множества В и один или несколько элементов множества В ставятся в соответствие элементу А:

1) Взаимно однозначное соответствие, когда каждому элементу 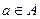ставится в соответствие единственный элемент 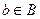и когда каждому элементу 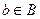соответствует только один элемент .

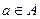2) Одно-многозначное соответствие, когда каждому элементу 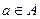ставится в соответствие несколько (более одного) элементов множества В, но каждому элементу 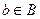соответствует только один элемент .

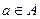3) Много-однозначное соответствие, когда для каждого элемента 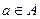существует только один элемент 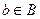, но каждому элементу множества В соответствует более одного элемента множества А.

4) Много-многозначное соответствие, когда каждому элементу 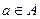соответствует более одного элемента множества В и каждому элементу 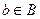соответствует также более одного элемента множества А.

Множество, равномощное множеству всех натуральных чисел, называется счетным.

Мощность счетного множества обозначается символом читается: алеф нуль. Алеф первая буква финикийского (древнесемитского) алфавита.

Кардинальное число конечного множества А обозначается |A|. Это обозначение будем использовать и в случае бесконечных множеств. Например, если Е – счетное множество, то |E| = .

При ведем некоторые теоремы о счетных множествах.

Теорема 1. Всякое бесконечное множество содержит счетное подмножество.

Теорема 2. Всякое бесконечное подмножество счетного множества счетно.

Теорема 3. Множество всех целых чисел счетно.

Теорема 4. Объединение счетного множества В счетно.

Теорема 5. Объединение конечного множества счетных множеств счетно.

Теорема 6. Декартово произведение двух счетных множеств А и В счетно.

Теорема 7. Объединение счетного множества счетных множеств A, B, C … счетно.

Теорема 8. множество всех рациональных чисел счетно. Рациональными называют все положительные и отрицательные дроби вида 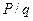, где P и q – натуральные числа. К рациональным относятся все целые положительные и отрицательные числа, а также нуль.

Теорема 9. множество всех алгебраических чисел счетно.

Несчетные множества.

Если А - конечное множество, то |A|<|B(A)|, то есть булеан всякого конечного множества А содержит больше элементов , чем множество А, т.к.

Всякое бесконечное множество также имеет подмножества и можно говорить о мощности его булеана.

Множество всех двоичных чисел бесконечной длины, представляется кардинальным числом

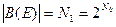
Теорема. Мощность булеана бесконечного множества Е превышает мощность множества Е. Это очень важная теорема. Если Е – счетное множество, то согласно приведенной теореме

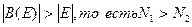
Множество В(Е) несчетно и его мощность равна мощности континуума (continuum – в переводе с латинского - непрерывное). Примером континуума может служить множество точек отрезка.

Несчетным является и множество всех действительных чисел в интервале . Для доказательства этого сначала предположим, что все действительные числа можно пронумеровать. Запишем одна под другой бесконечные десятичные дроби:

…

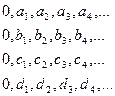
Получим матрицу, содержащую четное множество строк, в каждой из которых бесконечное число десятичных цифр. Допустим, что в матрице нет не одной пары равных между собой чисел. Все ли действительные числа окажутся в матрице? Нет, не все. Чтобы убедится в этом воспользуемся диагональным методом, разработанным Г. Кантором, и найдем число, которое соответствует матрице, т.е. оказалось незанумерованным. Суть метода Г. Кантора применительно к данному случаю состоит в следующем. Если в первом числе первая после запятой цифра (цифра ) не равна, например, 3, то в искомое число после запятой записываем цифру 3. Если же =3, то записываем, допустим 2. Переходя ко второму числу матрицы. Если , то записываем на втором месте искомого числа цифру 3. Если , то записываем число 2. Перейдя к третьему числу, записываем искомое число 3, если и т.д. Очевидно что получившееся число отсутствует в списке, так как оно отличается от первого числа после запятой цифрой, от второго числа отличается цифрой от третьего – третьей и т.д. Таким образом полученное число отсутствует в списке, но принадлежит множеству действительных чисел интервала .

Полученное число не является единственным отсутствующим в списке. Достаточно вместо цифры 3 и 2 взять какие-нибудь другие и мы получим еще одно число. Даже если найденные числа включит в общий список, то и в расширенном списке будут находится не занумерованные числа.

Так как мощность булеана В(Е) равна мощности множества всех действительных чисел интервала , то эти множества эквивалентны. Они являются несчетными и оба характеризуются кардинальным числом . Такие множества условно называют -множествами.

Мощность континуума – не самая большая мощность среди бесконечных множеств. Что бы убедится в этом воспользуемся двоичными числами, так же как и в случае с счетными множествами. Поставим в соответствие каждому элементу -множества двоичный разряд. Если единица в числе обозначает вхождение элемента в подмножество, а нуль – отсутствие элемента в данном подмножестве, то каждому двоичному числу будет соответствовать некоторое подмножество -множества. Мощность множества таких подмножеств обозначается буквой , очевидно, что

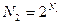
Откуда следует что мощность булеана -множества превышает мощность -множества .

Точно так же можно утверждать, что

То есть мощность -множества превышает мощность булеана -множества. Далее по аналогии получаем :

, , ,…, ,…

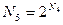Откуда следует, что множества с наибольшей мощностью не существует.

В завершение подраздела приведем одну теорему о множествах мощности континуума: объединение множества мощности континуума и счетного множества имеет мощность континуума.

Под нечётким множеством A понимается совокупность

, где Х — универсальное множество, а 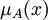— функция принадлежности (характеристическая функция), характеризующая степень принадлежности элемента нечёткому множеству А .

Функция 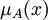принимает значения в некотором вполне упорядоченном множестве М. Множество М называют множеством принадлежностей, часто в качестве М выбирается отрезок . Если , то нечёткое множество может рассматриваться как обычное, чёткое множество.

Упражнения для выполнения:

Дата добавления: 2015-07-26; просмотров: 298; Нарушение авторских прав

Мы поможем в написании ваших работ!