
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Понятие непрерывности функции в точке
Постановка задачи. Пользуясь определением, доказать, что функция  непрерывна в точке
непрерывна в точке 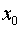 .
.
План решения.
Функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если 
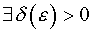 :
:  . Это значит, что
. Это значит, что  неравенство
неравенство 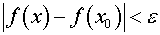 имеет решение
имеет решение  .
.
Задача 8. Доказать, что функция  непрерывна в точке
непрерывна в точке 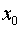 (найти
(найти 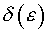 ).
).
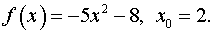
Покажем, что при любом  найдется такое
найдется такое 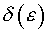 , что
, что 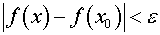 при
при  .
.
Имеем
 .
.
Следовательно
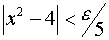 ,
,
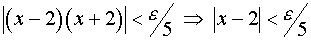 .
.
Т.е. неравенство 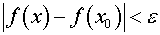 выполняется при
выполняется при 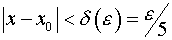 .
.
Вычисление пределов вида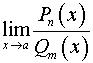
Постановка задачи. Вычислить предел
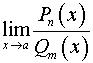 ,
,
где
 ,
,
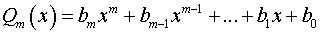 .
.
План решения.
1. Возможны три случая.
1) Если 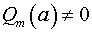 , то функция
, то функция 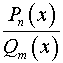 непрерывна в точке
непрерывна в точке  и
и
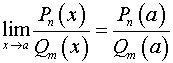 .
.
2) Если  и
и  , то
, то
 .
.
3) Если  и
и  , то разлагая многочлены на множители, получаем
, то разлагая многочлены на множители, получаем
 ,
,
где 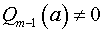 и
и  .
.
2. Поскольку в определении предела функции при  аргумент не может принимать значение, равное
аргумент не может принимать значение, равное  , то в последнем случае можно сократить множитель
, то в последнем случае можно сократить множитель 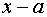 . Получаем
. Получаем
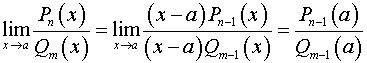 .
.
Замечание. Если число  является кратным корнем многочленов
является кратным корнем многочленов 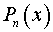 и
и 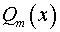 , то
, то  ,
, 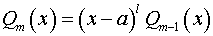 и
и
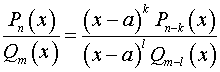 ,
,
где  и
и  . В зависимости от чисел
. В зависимости от чисел  и
и 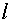 получим один из трех перечисленных в первом пункте случаев.
получим один из трех перечисленных в первом пункте случаев.
Задача 9. Вычислить пределы функций.
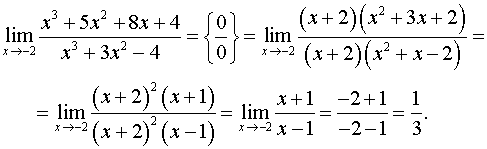
Вычисление пределов вида 
Постановка задачи. Вычислить предел
 ,
,
где  и
и  – бесконечно малые функции в точке
– бесконечно малые функции в точке  .
.
План решения.
Способ 1. Непосредственное вычисление пределов.
В зависимости от примера необходимо воспользоваться приемом домножения числителя и знаменателя на сопряженное выражение (если в дроби присутствуют радикалы) либо одной из следующих формул, приведя предварительно выражение к соответствующему виду:
 ,
,
 (первый замечательный предел),
(первый замечательный предел),
 (второй замечательный предел),
(второй замечательный предел),
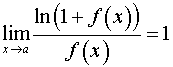 ,
,
 ,
,
 .
.
Во всех приведенных выше формулах 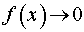 при
при 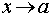 .
.
Способ 2. Замена на эквивалентные бесконечно малые.
1. Нужно заменить  и
и  на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки
на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки  . Поэтому сначала сделаем замену переменной
. Поэтому сначала сделаем замену переменной  и будем искать предел при
и будем искать предел при  (если
(если  , то замену делать не надо).
, то замену делать не надо).
2. Преобразуем выражение под знаком предела, пользуясь алгебраическими и тригонометрическими формулами, и заменяем в произведении и частном бесконечно малые функции эквивалентными.
Таблица эквивалентных бесконечно малых:
| Функция | Эквивалентная бесконечно малая |

| 
|

| 
|

| 
|
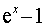
| 
|

| 
|

| 
|

| 
|
Задача 10.Вычислить пределы функций.
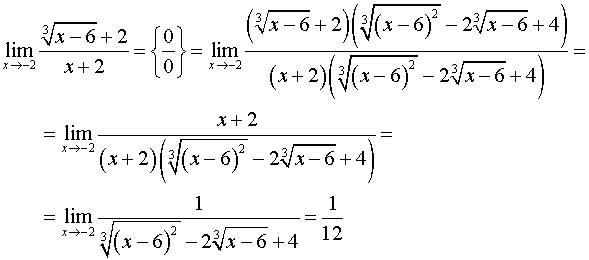
Вычисление пределов вида 
Постановка задачи. Вычислить предел
 ,
,
где  и
и  – бесконечно малые функции в точке
– бесконечно малые функции в точке  .
.
План решения.
Способ 1. Непосредственное вычисление пределов.
В зависимости от примера необходимо воспользоваться приемом домножения числителя и знаменателя на сопряженное выражение (если в дроби присутствуют радикалы) либо одной из следующих формул, приведя предварительно выражение к соответствующему виду:
 ,
,
 (первый замечательный предел),
(первый замечательный предел),
 (второй замечательный предел),
(второй замечательный предел),
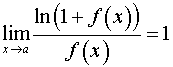 ,
,
 ,
,
 .
.
Во всех приведенных выше формулах 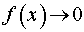 при
при 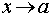 .
.
Способ 2. Замена на эквивалентные бесконечно малые.
1. Нужно заменить  и
и  на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки
на эквивалентные им бесконечно малые функции. Но таблица эквивалентных бесконечно малых функций составлена для точки  . Поэтому сначала сделаем замену переменной
. Поэтому сначала сделаем замену переменной  и будем искать предел при
и будем искать предел при  (если
(если  , то замену делать не надо).
, то замену делать не надо).
2. Преобразуем выражение под знаком предела, пользуясь алгебраическими и тригонометрическими формулами, и заменяем в произведении и частном бесконечно малые функции эквивалентными.
Таблица эквивалентных бесконечно малых:
| Функция | Эквивалентная бесконечно малая |

| 
|

| 
|

| 
|
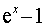
| 
|

| 
|

| 
|

| 
|
Задача 11. Вычислить пределы функций.
| <== предыдущая страница | | | следующая страница ==> |
| Понятие предела функции | | | Способ 1 |
Дата добавления: 2015-07-26; просмотров: 193; Нарушение авторских прав

Мы поможем в написании ваших работ!