
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Поиск экстремумов функций многих переменных
Можно выделить класс нелинейных задач, которые относятся к классическим методам оптимизации. В этом случае задачу оптимизации можно сформулировать так:
Найти переменные x 1,x2 ,…,xn, удовлетворяющие системе уравнений 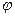 I(x1 ,x 2,…,xn) =bi ,i=
I(x1 ,x 2,…,xn) =bi ,i= 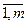 и обращающие в максимум (минимум) целевую функцию z=f(x1 ,x2 ,…,xn) при условии, что функции
и обращающие в максимум (минимум) целевую функцию z=f(x1 ,x2 ,…,xn) при условии, что функции 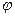 I(x) и f(x) непрерывны и имеют частные производные, по крайней мере, второго порядка. Примером типичной и простой нелинейной задачи является следующая.
I(x) и f(x) непрерывны и имеют частные производные, по крайней мере, второго порядка. Примером типичной и простой нелинейной задачи является следующая.
Объем производства, выраженный в натуральных или стоимостных единицах, является функцией затрат производства z=f(x1,x2). Эта зависимость называется производственной функцией. Издержки зависят от расхода обоих факторов(x1 и x2) и от цен этих факторов (c1 и c2). Совокупные издержки выражаются формулой b= с1x1+c2x2. Требуется при данных совокупных издержках определить такое количество факторов производства(например, машины и труд, два розничных вида сырья и т.д.), которое максимизирует объем продукции z.
Математическая модель этой задачи имеет вид: определить такие переменные x1 и x2, удовлетворяющие условиям c1x1+c2x2=b; x1 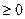 и x2
и x2 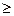 0, при которых функция z=f(x1,x2) достигает максимума. Как правило, эта функция имеет произвольный нелинейный вид.
0, при которых функция z=f(x1,x2) достигает максимума. Как правило, эта функция имеет произвольный нелинейный вид.
Используя классические методы оптимизации, следует четко представлять различие между локальным, глобальным и условным экстремумом.
Первые два понятия были рассмотрены достаточно подробно во втором разделе курса, поэтому здесь дадим определение только условного
экстремума.
Разъясним это понятие на примере нелинейной функции двух переменных.
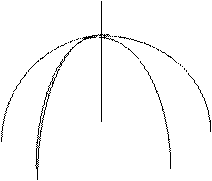
Возьмем функцию z=  , графиком которой является верхняя полусфера.
, графиком которой является верхняя полусфера.
Y
 |
 M
M
 M1
M1








 0 В Z
0 В Z
pP
A P
X
Рис. 10. График функции z = 
Эта функция имеет максимум в начале координат, которому соответствует точка M. Проведем линию AB, проходящую через точки пересечения полусферы с координатными осями. Эта линия L 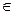 {A,B}, лежащая в плоскости 0XZ вычисляется по уравнению x+y-1=0 или y=1-x, которое называется уравнением связи. Из геометрического представления функции следует, что для точек этой линии L наибольшее значение функции достигается в точке P(
{A,B}, лежащая в плоскости 0XZ вычисляется по уравнению x+y-1=0 или y=1-x, которое называется уравнением связи. Из геометрического представления функции следует, что для точек этой линии L наибольшее значение функции достигается в точке P( 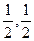 ), лежащей посередине отрезка AB. Это и есть точка условного экстремума функции z=
), лежащей посередине отрезка AB. Это и есть точка условного экстремума функции z=  . Ей соответствует точка M1 на полусфере.
. Ей соответствует точка M1 на полусфере.
Для отыскания точек условного экстремума поступают следующим образом:
1.Если из уравнения связи y=  (x) можно явно выразить одну независимую переменную через другую, то, подставляя в выражение функции y=f(x,y) вместо y функцию
(x) можно явно выразить одну независимую переменную через другую, то, подставляя в выражение функции y=f(x,y) вместо y функцию  получим функцию одной переменной
получим функцию одной переменной
Z = f[x,  (x)]=
(x)]=  (x).
(x).
2.Найдя значения x*i, при которых эта функция достигает экстремума, и определив затем из уравнения связи  (x) соответствующие значение y, получим искомые точки условного экстремума.
(x) соответствующие значение y, получим искомые точки условного экстремума.
Таким образом, для того, чтобы найти точки, которые могут быть точками условного экстремума функции z=f(x,y) при известном уравнении связи  (x,y)=0, необходимо образовать вспомогательную функцию
(x,y)=0, необходимо образовать вспомогательную функцию  (x,y)=f(x,y)+
(x,y)=f(x,y)+ 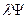 (x,y), составить и решить уравнения для отыскания точек экстремума этой функции
(x,y), составить и решить уравнения для отыскания точек экстремума этой функции  (x,y). Описанный прием решения задач на условный экстремум в более общей постановке называется методом множителей Лагранжа, который будет рассмотрен в пятом разделе. Данный раздел целиком ориентирован на изучение задач нелинейного программирования.
(x,y). Описанный прием решения задач на условный экстремум в более общей постановке называется методом множителей Лагранжа, который будет рассмотрен в пятом разделе. Данный раздел целиком ориентирован на изучение задач нелинейного программирования.
Суть классической теории сводится к следующему. Будем полагать , что многомерная функция z = f(x1,x2,…xn) = f(x) дважды дифференцируема в точке x*=(x*1,x*2,…,x*n), x* 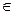 D(f) и в некоторой ее
D(f) и в некоторой ее  -окрестности. Если для всех точек этой окрестности f(x*)
-окрестности. Если для всех точек этой окрестности f(x*)  f(x), то говорят, что функция f(x) имеет экстремум в x*.Точка x*, в которой все частные производные функции z=f(x)’ равны нулю, называется стационарной точкой.
f(x), то говорят, что функция f(x) имеет экстремум в x*.Точка x*, в которой все частные производные функции z=f(x)’ равны нулю, называется стационарной точкой.
Необходимое условие экстремума. Если в точке x* функция z=f(x) имеет экстремум, то частные производные в этой точке равны нулю.
Геометрически это выражается в том, что касательная плоскость к поверхности - графику функции в соответствующей ее точке – параллельна плоскости независимых переменных.
Также как и для функций одной переменной, необходимый признак экстремума в случае многих переменных не является достаточным. Приведем условия достаточности без доказательства для функций двух переменных.
Пусть точка P0(x0,y0) является стационарной точкой функции z=f(x,y), т.е.( 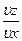 )0=0 и (
)0=0 и ( 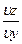 )0=0. Вычислив значения вторых частных производных функции f(x,y) и обозначив их через A,B и C: A=(
)0=0. Вычислив значения вторых частных производных функции f(x,y) и обозначив их через A,B и C: A=(  )0 , B=(
)0 , B=( 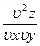 )0 , C=(
)0 , C=( 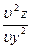 )0.
)0.
Если B2-AC  0, то функция f(x,y) имеет в точке P0(x0,y0) экстремум: максимум при A
0, то функция f(x,y) имеет в точке P0(x0,y0) экстремум: максимум при A  0 и C
0 и C  0 минимум при A
0 минимум при A  0 и C
0 и C  0.
0.
Если B2-AC  0, то точка P0 не является точкой экстремума.
0, то точка P0 не является точкой экстремума.
Если B2-AC=0, то никакого заключения о характере стационарной точки сделать нельзя и требуется дополнительное исследование.
Следовательно, чтобы найти экстремальное значение функции z=f(x,y) в области D, нужно:
1) найти все стационарные точки внутри области D и вычислить значения функции в них;
2) исследовать функцию на экстремум на границе области D;
3) сравнить значения функции, полученные в п.1 и 2:
наибольшее (наименьшее) из этих чисел и будет наибольшим (наименьшим) значением функции во всей области. Граница области D аналитически может быть задана системой уравнений (условий) относительно переменных x1,x2,…,xn. Поэтому, исследуя экстремальные свойства функции на границе, необходимо решить задачу условного экстремума (см. подраздел 3.1).
Другой способ определения условного экстремума начинается с построения вспомогательной функции Лагранжа, которая в области допустимых решений достигает максимума для тех же значений переменных x1,x2,…,xn и что и целевая функция z.
Пусть решается задача определения условного экстремума функции z=f(x) при ограничениях 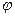 I(x1,x2…,xn) =0, i=
I(x1,x2…,xn) =0, i= 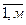 ,m
,m  n, которые называются уравнениями связи.
n, которые называются уравнениями связи.
Составим функцию L(x)=f(x)+ 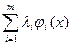 , которая называется функцией Лагранжа.
, которая называется функцией Лагранжа.
 - множители Лагранжа.
- множители Лагранжа.
Отметим, что множителям Лагранжа можно придать экономический смысл. Если f(x1,x2,…,xn) - доход, соответствующий плану x=(x1,x2,…,xn), а функция 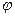 I(x1,x2,…,xn)- издержки i-го ресурса, соответствующие этому плану, то
I(x1,x2,…,xn)- издержки i-го ресурса, соответствующие этому плану, то 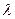 I- цена (оценка) i-го ресурса, характеризующая изменение экстремального значения целевой функции в зависимости от изменения размера i-го ресурса. L(x)-функция n+m переменных (x1,x2,…,xn,
I- цена (оценка) i-го ресурса, характеризующая изменение экстремального значения целевой функции в зависимости от изменения размера i-го ресурса. L(x)-функция n+m переменных (x1,x2,…,xn, 
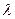 1,
1, 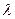 2,…,
2,…, 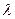 m).Определение стационарных точек этой функции приводит к решению системы уравнений
m).Определение стационарных точек этой функции приводит к решению системы уравнений
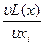 =0, (8)
=0, (8)
 =0, i=
=0, i= 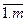
i= 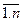
Легко заметить, что 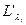 (x)=
(x)=  (x), т.е. в эту систему входят уравнения связи.
(x), т.е. в эту систему входят уравнения связи.
Таким образом, задача нахождения условного экстремума функции z=f(x) сводится к нахождению локального экстремума функции L(x). Если стационарная точка найдена, то вопрос о существовании экстремума в простейших случаях решается на основании достаточных условий экстремума- исследования знака второго дифференциала d2L(x) в стационарной точке.
В заключении отметим, что описанные выше классические методы оптимизации имеют весьма ограниченное применение. Хотя бы потому, что задача получения условного экстремума функции и переменных весьма трудоемка. Более того классические методы вообще не работают, если множество допустимых значений аргумента дискретно или целевая функция задана таблично. Если критерий эффективности задан нелинейной функцией, то имеет задачу нелинейного программирования. В частности, или указанные функции обладают свойствами выпуклости, то полученная задача является задачей выпуклого программирования.
| <== предыдущая страница | | | следующая страница ==> |
| Многомерная оптимизация без ограничений | | | Выпуклый анализ |
Дата добавления: 2015-07-26; просмотров: 256; Нарушение авторских прав

Мы поможем в написании ваших работ!