Выпуклый анализ

В школьном курсе математики выпуклыми назывались многоугольники, целиком расположенные по одну сторону от прямых, на которых лежат их стороны.

B C

B D

M

N М N

А

C

а) D

A E

Е б)

Рис. 11. Примеры выпуклого (а) и невыпуклого (б) множеств

Например, многоугольник а)- выпуклый, многоугольник б)- не является выпуклым (он расположен по обе стороны от прямой BC).

Общим определяющим свойством, которое отличает выпуклый многоугольник от невыпуклого, является то, что если взять любые две точки и соединить их отрезком, то весь отрезок будет принадлежать этому многоугольнику. Это свойство может быть принято за определение выпуклого множества точек.

Определение.Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержат весь отрезок, соединяющий эти точки.

Примерами выпуклых множеств являются также круг, сектор, отрезок, куб, пирамида.

Наряду с выпуклым множеством в теории оптимизации пользуютсяпонятие и выпуклой функции.

Определение.Функция F(x)=F(x₁,x₂,..,x_n), определенная на выпуклом множестве М n- мерного пространства, называется выпуклой на этом множестве, если

F( x₁+(1- )x₂) F(x₁)+(1- )F(x₂) (3.2.1)

Для любых точек x₁,x₂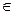 Mи любого числа .

F(x)

F(x₂)

F(x)

F(x₁)

0 x₁ x= x₁+(1- ) X₂ X₂ X

Рис. 12. График выпуклой функции

На этом рисунке изображен график функции одной переменной, выпуклой на всей числовой прямой.

Для любой пары x₁ и x₂ значений аргумента произвольную точку можно задать в виде x= x₁+(1- )x₂.

Как видно из этого рисунка неравенство (3.2.1) означает, что отрезок, соединяющий точки x₁; F(x₁) и x₂; F(x₂) расположен не ниже графика функции на этом участке.

Рассмотрим свойства выпуклой функции.

Алгебраические и аналитические свойства выпуклых функций

1. Если функция F(x)- выпукла, то функция – F(x) вогнута.

2. Если функция F(x)=C и линейная функция F(x)=ax+b являются всюду выпуклыми и всюду вогнутыми.

3. Если функции F_i(x), i= 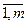, выпуклы, то при любых действительных числах a_i 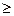0 функция 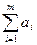F_i(x) также является выпуклой.

4. Если функция F(x) выпукла, то для любого числа a область решения неравенства F(x) a является выпуклым множеством, либо пустым.

5. Если функция (x) выпуклы при всех неотрицательных значениях переменных, то область решений системы неравенств 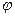_I(x) b, i= 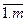является выпуклым множеством (если она не пуста).

6. Выпуклая (вогнутая) функция, определенная на выпуклом множестве М, непрерывна в каждой внутренней точке этого множества.

7. Всякая дифференцируемая строго выпуклая (вогнутая) функция имеет не более одной стационарной точки (т.е. точки, в которой все частные производные равны нулю).При этом для выпуклой (вогнутой) функции стационарная точка всегда является точной локального и глобального экстремума.

Свойство выпуклости функций широко используется при решении задач оптимизации, которые относятся к классу задач выпуклого программирования.

Дата добавления: 2015-07-26; просмотров: 228; Нарушение авторских прав

Мы поможем в написании ваших работ!