Градиент и матрица Гессе функции многих переменных

Общая схема решения задач данным методом состоит в построении последовательности x₀,x₁,x₂,…,x_n решений системы ограничений по следующему принципу: в качестве x₀ выбирается, вообще говоря, любая точка области решений и затем каждая последующая получается из предыдущей по формуле

X_k+1=x_k+ ,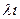

Где -некоторое направление (т.е. вектор), 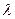- некоторое число.

При это направление и “длина шага” выбираются так, чтобы обеспечить сходимость процесса оптимального решения x*.

Для реализации данного метода необходимо вычислить градиент функции по данному направлению.

Напомним, что градиентом функции (для случая трех переменных) и (x,y,z) называется вектор, проекциями которого служат значения частных производных этой функции, т.е.

gradu= .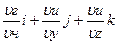

Пользуясь этим определением, можно записать 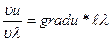, т.е. производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления.

Или производная функции по данному направлению равна проекции градиента функции на направление дифференцирования, т.е. . Отсюда следует, что производная по направлению 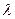достигает наибольшего значения, когда Сos 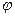=1, т.е. 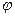=0

Z

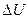
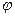
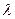
p

0 Y

X

Рис. 14. Градиент функции

Таким образом, направление градиента есть направление наискорейшего возрастания функции. В противоположном направлении функция U будет быстрее всего убывать.

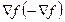Находя частную производную по направлению , мы можем определить, является ли направление “невыгодным” или “выгодным” в смысле приближения к оптимуму. Так как направление градиента f целевой функции является направлением ее наискорейшего роста, то при отыскании max вогнутой функции (min выпуклой функции) в качестве часто берется и тогда формула (*) принимает вид:

X_k+1=x_k+ - если ищется максимум и x_k+1=x_k- - если ищется минимум.

Методы спуска, в которых интеграционная последовательность x₀,x₁,x₂,…,x_k,… находится по этим формулам x_k+1=x_{k 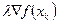,} называются градиентными. К их числу относятся, в частности, широко используемый в практике метод наискорейшего спуска. Для случая функции двух переменных метод наискорейшего спуска имеет простейшую интерпретацию (рис.18).

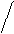
F

X^*

X₁ Х₃ x₄

X₂

X₀

Х

Рис. 15. Линии уровня

На этом рисунке изображены линии уровня некоторой функции F(x,y,z), для которых, как известно f=const.

Отсюда видно, что для любого k луч, идущий от точки x_k к точке x_k+1 перпендикулярен к линии уровня функции f, проходящей через точку x_k (т.к. направлен по градиенту), и касается следующей линии уровня, проходящей через точку x_k+1. Таким образом, на плоскости наискорейший спуск происходит по двум взаимно перпендикулярным направлениям.

В заключении отметим, что для метода градиентного спуска величина шага вдоль выбранного направления постоянна для каждой итерации, а для метода наискорейшего спуска характерен переменный шаг.

Дата добавления: 2015-07-26; просмотров: 271; Нарушение авторских прав

Мы поможем в написании ваших работ!