
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Графическая и экономическая интерпретация задач оптимизации
Рассмотрим задачу планирования производства, иначе - задачу об использовании ресурсов в линейной обстановке.
В обобщенной постановке задача имеет вид:
Найти такой план x выпуска продукции, удовлетворяющий системе:
 |
a11x1+a12x2+…+a1nxn  b1
b1
a21x2+a22x2+…+a2nxn  b2 (9)
b2 (9)
……………….
an1x1+an2x2+…+annxn  bn
bn
и условий X1 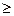 0, X2
0, X2 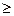 0…..,Xn
0…..,Xn 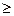 0 ,
0 ,
при которых функция F=с1х1+с2х2+…+с4х4 принимает максимальное значение.
Это и есть общая задача линейного программирования, где F есть линейная функция, линейная форма, целевая функция или функция цели. Если система ограничений состоит из неравенств, то задача называется стандартной, если из равенств, то задача называется канонической. Любая форма линейного программирования может быть сведена к канонической, стандартной или общей формам.
Рассмотрим пример.
Для изготовления двух видов продукции Р1 и Р2 используют четыре вида ресурсов S1, S2, S3, S4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 3.
Таблица 3
| Вид ресурса | Запас ресурса | Число единиц ресурсов, затрачиваемое на изготовление единицы продукции | |||
| P1 | P2 | ||||
| S1 | |||||
| S2 | |||||
| S3 | _ | ||||
Прибыль получаемая от реализации продукции Р1 и Р2 соответственно 2 и 3 рубля. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации максимальной.
Решение. Составим экономико-математическую модель задачи.
 Обозначим х1 и х2 – число единиц продукции соответственно, Р1 и Р2 запланированных к производству. Для их изготовления (см. таблицу) потребуется(1х1 +3х2) единиц ресурса S1, (2х1+1х2) единиц ресурса S2, (1х2)- единиц S3 и (3х1)- единиц ресурсовS4.Так как потребление ресурсов не должно превышать их запасы , то связь между ними можно выразить с помощью следующих неравенств.
Обозначим х1 и х2 – число единиц продукции соответственно, Р1 и Р2 запланированных к производству. Для их изготовления (см. таблицу) потребуется(1х1 +3х2) единиц ресурса S1, (2х1+1х2) единиц ресурса S2, (1х2)- единиц S3 и (3х1)- единиц ресурсовS4.Так как потребление ресурсов не должно превышать их запасы , то связь между ними можно выразить с помощью следующих неравенств.
Очевидно, что при F=0 линия уровня 2х1+ 3х2=0 проходит через начало координат (строить ее необязательно). Зададим, например F=6 и построим линию уровня 2х1+ 3х2=6. Ее расположение в плоскости ОХ1Х2 указывает на направление возрастания линейной функции( вектор 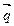 ). Так как по условию задачи необходимо найти максимум, то как следует из графика он должен находится в угловой точке С, находящейся на пересечении прямых ׀ и ׀׀. Это означает, что координаты точки С определяются решением системы
). Так как по условию задачи необходимо найти максимум, то как следует из графика он должен находится в угловой точке С, находящейся на пересечении прямых ׀ и ׀׀. Это означает, что координаты точки С определяются решением системы
 х1+ 3х2=18
х1+ 3х2=18
2х1+х2=16,
откуда х1=6, х2=4;т.е. С(6;4).
Максимум линейной функции равен F=2 6 + 3 4 =24. Итак, Fmax =24 при оптимальном решении х1=6, х2=4, т.е. максимальная прибыль в 24 рубля может быть достигнута при производстве Р1=6 и Р2=4. В этой задаче max F достигался в одной точке и задача имела одно оптимальное решение (рис.19).

 |



 8
8




 6 A B
6 A B


 4 C
4 C






 2
2 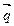 D E
D E  F=Fmax=24
F=Fmax=24



















 X1
X1
0  2 4 6
2 4 6  F=8
F=8
 F=6
F=6
Рис. 16. Многоугольник ограничений
Между тем в экономической практике нередко встречаются задачи, в которых эти условия не удовлетворяются, т. е. может наблюдаться не одно, а множество решений, которые требуют тщательного рассмотрения конкретных ситуаций.
| <== предыдущая страница | | | следующая страница ==> |
| Градиент и матрица Гессе функции многих переменных | | | Метод множителей Лагранжа, их экономический смысл |
Дата добавления: 2015-07-26; просмотров: 235; Нарушение авторских прав

Мы поможем в написании ваших работ!