
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Графический метод решения задачи нелинейного программирования
Графический метод решения задачи нелинейного программирования принимается в случае двух переменных.
Напомним, (см. раздел 3, подраздел 3.2), что множество точек называется выпуклым, если оно вместе с любыми своими двумя точками содержит и весь отрезок, соединяющий эти точки. Если [a;b]- отрезок на числовой прямой и x 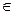 [a;b], то при 0
[a;b], то при 0 
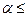 1, x=
1, x=  а + (1-
а + (1-  )b, или x=
)b, или x= 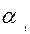 a +
a + 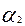 b при
b при 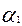 +
+ 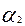 =1 и
=1 и 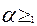 0 и
0 и  0. По определению функция F(X)=F(x1,x2,…,xn) определенная на выпуклом множестве М n –го пространства называется выпуклой на этом множестве, если F(
0. По определению функция F(X)=F(x1,x2,…,xn) определенная на выпуклом множестве М n –го пространства называется выпуклой на этом множестве, если F(  x1+(1-
x1+(1-  ) x2)
) x2) 
 F(x1)+(1-
F(x1)+(1-  )F(x) (13)
)F(x) (13)
Для любых точек х1, х2, 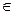 М и любого числа
М и любого числа  (-[0:1]).Сказанное из рассмотрения графика выпуклой функции. То есть значение выпуклой функции в промежуточной точке х всегда не меньше ее значений на границе рассматриваемого интеграла. Для вогнутой функции знак неравенства не меняется на противоположный.
(-[0:1]).Сказанное из рассмотрения графика выпуклой функции. То есть значение выпуклой функции в промежуточной точке х всегда не меньше ее значений на границе рассматриваемого интеграла. Для вогнутой функции знак неравенства не меняется на противоположный.
 F(x) Примечание. Множество всех точек
F(x) Примечание. Множество всех точек
 X=(x1, x2, …,xn) образует n- мерное точеч
X=(x1, x2, …,xn) образует n- мерное точеч
ное пространство. При n>3 точки и фигу-




 F(x2) ры n-мерного пространства не имеют реа-
F(x2) ры n-мерного пространства не имеют реа-

 льного геометрического смысла.
льного геометрического смысла.
F(x1) F(x)

 x1 x2
x1 x2
x= 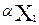 + (1 -
+ (1 -  )x2
)x2
Рис. 17. Выпуклая функция
Использование графического метода предопределяет вычисление и построение линий уровня, которыми называется множество всех точек (x;y), в которых функция принимает постоянное значение. В случае линейной функции все линии уровня представляют собой прямые , перпендикулярные общему вектору нормали.
В общем случае задачи выпуклого программирования являются задачами нелинейного программирования. Выделение задач выпуклого программирования в специальный класс объясняется экстремальными свойствами выпуклых функций: всякий локальный минимум выпуклой функции (локальный максимум вогнутой функции) является одновременно и глобальным; кроме того ввиду 2-го свойства (см. Подраздел 3.2) выпуклая (вогнутая) функция, заданная на ограниченном множестве достигает на нем глобального минимума (максимума), отсюда вытекает: если целевая функция Z является строго выпуклой (строго вогнутой) и если область решений системы ограничений
не пуста и ограничена, то задача выпуклого программирования всегда имеет единственное решение. В этом случае минимум выпуклой (максимум вогнутой) функции достигается внутри области решений, если там имеется стационарная точка, или на границе этой области – если внутри ее стационарная точка отсутствует.
Алгоритм решения задачи нелинейного программирования графическим методом предусматривает выполнение следующих процедур:
1.Рассматривается множество всех допустимых решений на основе системы ограничений вида
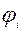 (x1,x2,..xn)
(x1,x2,..xn)  bi, i=
bi, i= 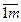 . (
. ( 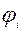 (x1,x2,)
(x1,x2,)  bi, I=
bi, I=  ) и в системе координат OX, х2 строится это множество.
) и в системе координат OX, х2 строится это множество.
2.Проверка множества на предмет пустого x= 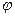 ,если оно пусто , то задача неразрешима. M=
,если оно пусто , то задача неразрешима. M= 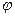 , что множество М не имеет ни одного элемента (такие множества называются пустыми).
, что множество М не имеет ни одного элемента (такие множества называются пустыми).
3.Если М 
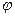 , то необходимо рассчитать, вычислить и построить линии уровня f=a при монотонном изменении u от -
, то необходимо рассчитать, вычислить и построить линии уровня f=a при монотонном изменении u от - 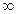 до +
до + 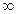 .Напомним, что линией уровня целевой функции Z= f(x;y) называется линия на плоскости OXY в которой функция сохраняет постоянное значение. Совокупность линий уровня, соответствующих различным сечениям – называется сетью, которая наглядно графически характеризует поведение целевой функции .( Примеры: изобары и изотермы – метеорология , горизонтали, топография(рельеф) , изокванты – экономика и др. ) При увеличении u линия Z=(x;y)=a смещается эквидистантно в направлении вектора q , нормального в данной точке к линии уровня. При этом , если А - первая точка встречи линии уровня с областью X, Y, f(x;y)=a0 то линия уровня f(x;y)=a при а<a0 не имеет общих точек с областьюXY.Отсюда следует, что а0=min f наX,Y. Аналогично, если А- последняя точка пересечения линии уровня с областью X,Yто f(A)=max fна X,Y. Таким образом из графического представления видно, имеются ли у допустимого множества вершины, имеет она решение или нет. Если у области f
.Напомним, что линией уровня целевой функции Z= f(x;y) называется линия на плоскости OXY в которой функция сохраняет постоянное значение. Совокупность линий уровня, соответствующих различным сечениям – называется сетью, которая наглядно графически характеризует поведение целевой функции .( Примеры: изобары и изотермы – метеорология , горизонтали, топография(рельеф) , изокванты – экономика и др. ) При увеличении u линия Z=(x;y)=a смещается эквидистантно в направлении вектора q , нормального в данной точке к линии уровня. При этом , если А - первая точка встречи линии уровня с областью X, Y, f(x;y)=a0 то линия уровня f(x;y)=a при а<a0 не имеет общих точек с областьюXY.Отсюда следует, что а0=min f наX,Y. Аналогично, если А- последняя точка пересечения линии уровня с областью X,Yто f(A)=max fна X,Y. Таким образом из графического представления видно, имеются ли у допустимого множества вершины, имеет она решение или нет. Если у области f 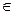 (x;y) есть хотя бы одна вершина, то (при ограниченной целевой функции) оптимальное значение может быть найдено методом перебора вершин. Для вычисления целевой функции в некоторой вершине допустимого множества необходимо знать точное значение ее координат, определение которых осуществляется решением ограничений
(x;y) есть хотя бы одна вершина, то (при ограниченной целевой функции) оптимальное значение может быть найдено методом перебора вершин. Для вычисления целевой функции в некоторой вершине допустимого множества необходимо знать точное значение ее координат, определение которых осуществляется решением ограничений  (11)
(11)
где I и j – номера линий ограничивающих область D(x;y), на пересечении которых находится искомая вершина. Основным преимуществом графического метода является ,то что он позволяет избежать полного перебора вершин, т.е. нет необходимости вычислять координаты других вершин при обнаружении оптимального решения. Необходимо решить следующую задачу выпуклого программирования: найти минимум функции Z=2+(x1-1)2+(x2-1)2:
 при ограничении
при ограничении
x12+x22  4
4
x1  2x2
2x2
x2  2x1
2x1
x1 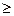 0, x2
0, x2 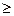 0
0
Решение. Строим область допустимых решений:
 а) x12+x22=4- окружность с центром в начале координат и радиусом R=2.
а) x12+x22=4- окружность с центром в начале координат и радиусом R=2.
Область решений неравенства x12+x22  4 состоит из точек, лежащих
4 состоит из точек, лежащих
внутри этой области окружности и на ее границе;


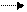
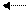









 x2 A
x2 A
В
 |
B x1
X1=2x2
X2=2x1
Рис. 18. График целевой функции
б) x1=2x2-прямая, которую можно построить, например , по точкам (0;0) и (2;1) область решений неравенства x1  2x2 – полуплоскость лежащая на этой прямой , включая и саму прямую;
2x2 – полуплоскость лежащая на этой прямой , включая и саму прямую;
в) x2=2x1- прямая , которая строится аналогично прямой x1=2x2 , только по точкам (0;0) и (1;2) .Область решений неравенства x2  2x1 - полуплоскость , лежащая под этой прямой , включая и саму прямую.
2x1 - полуплоскость , лежащая под этой прямой , включая и саму прямую.
Таким образом , с учетом условий не отрицательности переменных областью допустимых решений данной задачи является замкнутый сектор ОАВ.
Теперь построим линию уровня Z и определим направление ее убывания . По определению все линии уровня имеют уравнение Z=c т.е. (x1-1)2+(x2-1)2=C-2. Пусть const C=3. Тогда линия уровня (x1-1)2+(x2-1)2=1 –это окружность с центром в точке О1 (1;1) и радиусом r=1. Из рассмотрения представленных на рисунке графиков очевидно, что при перемещении от центра О1 к границе окружности функция возрастает и наоборот убывает (стрелками указано направление убывания функции Z). Таким образом минимум Z достигается в точке (1;1), а Zmin=2. Нетрудно убедиться, что точка(1;1) является стационарной точкой функции Z. Решение этой задачи предлагается студентам осуществить самостоятельно.
| <== предыдущая страница | | | следующая страница ==> |
| Метод множителей Лагранжа, их экономический смысл | | | Метод штрафных функций |
Дата добавления: 2015-07-26; просмотров: 276; Нарушение авторских прав

Мы поможем в написании ваших работ!