
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Условие Куна – Таккера
Пусть дана задача нелинейного программирования: найти максимальное значение функции 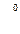 Z=f(x1, x2, …., xn)
Z=f(x1, x2, …., xn) 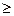 0, I=
0, I= 
Составим функцию Лагранжа для данной задачи
F(x, 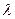 )=f(x)+
)=f(x)+ 
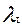 qi(x)
qi(x)  (14)
(14)
Если выполняется условие регулярности (т.е. существует по крайней мере одна точка Х, для которой qi(x)>0,то имеет место следующая теорема:


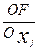 x0
x0 
 0; xj0
0; xj0  x0
x0  =0 , xj
=0 , xj 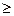 0, j=
0, j=  (21)
(21)
 x0
x0 
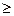 0 ;
0 ; 
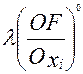 x0,
x0,  =0 , xi
=0 , xi 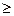 0, I=
0, I= 

Вектор Х0 тогда и только тогда является оптимальным решением задачи, когда, когда существует такой вектор  , что при x0
, что при x0 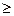 0 и
0 и 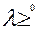 0 для всех х
0 для всех х 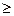 0 и
0 и 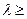 0.
0.
F(x, 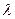 0)
0)  F(x0,
F(x0,  )
)  F(x0,
F(x0, 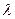 ). (15)
). (15)
Если f(x) и g(x) – дифференцируемые функции, то условие(2) эквивалентно следующим локальным условиям Куна-Танкера:
Выражение 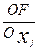 означает, что значение частной производной функции Лагранжа берется в точке x0,
означает, что значение частной производной функции Лагранжа берется в точке x0,  , где x0=(x10, x20, …,xn0) и
, где x0=(x10, x20, …,xn0) и  =(
=( 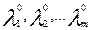 ).
).
Покажем применение условий Куна-Такера на следующем примере. Найти максимум функцию Z=-x12- x22 при ограничениях:
 2x1+x2
2x1+x2 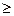 2
2
x1+x2  6
6
2x1+x2  8 x1
8 x1 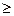 0, x2
0, x2 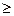 0
0  .
.
Решение:
1.Аналитически или с помощью графического метода можно определить x1=0,8, x2=0,4, Z=-0,8.
2.Покажем, что существует 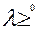 0, при которой в точке максимума выполняется условие Куна-Таккера.
0, при которой в точке максимума выполняется условие Куна-Таккера.
Для функции F(x, 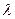 ):
):
F(x, 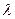 )=-x12-x22+
)=-x12-x22+ 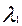 (2x1+x2-2)+
(2x1+x2-2)+  (-2x1-x2+8)+
(-2x1-x2+8)+ 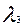 (6-x1-x2)
(6-x1-x2)
Находим частные производные
 =-2x1+2
=-2x1+2 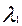 -2
-2  -
- 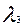 ;
; 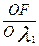 =2x1+x2-Z
=2x1+x2-Z
 =-2x2+
=-2x2+ 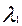 -
-  -
- 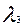 ;
;
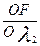 =8-2x1-x2;
=8-2x1-x2; 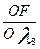 =6-x1-x2.
=6-x1-x2.
Согласно условиям (3)  и
и 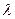 3 должны принимать нулевые значения т.к. подставляя x1=0,8 , x2=0,4 в выражение
3 должны принимать нулевые значения т.к. подставляя x1=0,8 , x2=0,4 в выражение 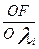 и
и 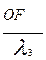 , имеет значение больше нуля, но с условием
, имеет значение больше нуля, но с условием 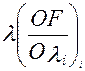 x0,
x0,  =0.
=0.
В соответствии с условием (2) производная 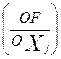 x0,
x0,  (j=1,2) должна принимать нулевое значение т.к. координаты вектора х0 отличны от нуля. Находим
(j=1,2) должна принимать нулевое значение т.к. координаты вектора х0 отличны от нуля. Находим 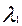 =0,8. Следовательно, в точке (х0,
=0,8. Следовательно, в точке (х0,  ) выполняются условия Куна - Таккера и она действительно является точкой экстремума.
) выполняются условия Куна - Таккера и она действительно является точкой экстремума.
| <== предыдущая страница | | | следующая страница ==> |
| Метод штрафных функций | | | Динамическое программирование. Общая постановка задачи |
Дата добавления: 2015-07-26; просмотров: 466; Нарушение авторских прав

Мы поможем в написании ваших работ!