Однокритериальные задачи

Тема 3. Принятие решений в условиях определенности

Тема 3. Принятие решений в условиях определенности. 1

3.1. Однокритериальные задачи. 1

3.2. Многокритериальные задачи принятия решений. 3

3.2.1. Построение интегральных критериев. 4

3.2.2. Примеры использования свертки критериев. 9

3.2.3. Комментарий Е.С.Вентцель [1] 10

3.2.4. Парето оптимальные решения. 12

3.3. Методы нахождения множества Парето. 14

3.4.Подход исследования операций. 18

3.5.Обсуждение многокритериальности. 19

3.6.Человекомашинные процедуры.. 20

3.6.1.Классификация ЧМП.. 20

3.6.2.Прямые человекомашинные процедуры.. 21

3.6.3.Процедуры оценки векторов. 21

3.6.4.Процедуры поиска удовлетворительных значений критериев. 22

3.6.5.Исследование решений на множестве Парето. 24

Библиографический список. 24

Контрольное задание. 24

Однокритериальные задачи

Рассмотрим вначале несколько примеров математических задач, подходя к ним как к задачам принятия решений.

Пример 3-1 (классический анализ). Чтобы попасть из пункта A в пункт В, экипаж должен проехать вначале по лугу, а затем по прямолинейному шоссе (рис. 3). Известно расстояние от А до шоссе и известны скорости экипажа по лугу и по шоссе. В каком месте экипажу надо выехать на шоссе, чтобы время переезда из A в В было минимальным?

Сформулированную задачу можно рассматривать как задачу принятия ре­шения: множество альтернатив состоит из множества точек прямой 0В (или из
множества действительных чисел, если ввести ось х, как показано на рис.3-1).
Каждой точке х соответствует исход -- маршрут АхВ.. Каждый исход (т.е.
маршрут) оценивается числом — временем поездки по этому маршруту. Таким образом, имеем задачу принятия решения в условиях определенности.

Пример 3-2 (линейное программирование). Имеется m пунктов А1,…,Am производства некоторого продукта и k пунктов B1,…,Bk потребления этого продукта. Количество данного продукта в пункте Ai равно ai, а потребность в нем в пункте Вj равна bj (i=1, ..., m; j=1, ..., k). Стоимость перевозки единицы продукта из Ai в Bj равна cij. Как следует спланировать перевозки, чтобы: а) вывезти весь продукт из пунктов производства, б) удовлетворить потребности пунктов потребления, и чтобы суммарная стоимость перевозок была наименьшей (стоимость перевозки продукта пропорциональна его количеству)?

Спланировать перевозки — это значит, для каждого пункта производства Аi и каждого пункта потребления Bj указать, какое количество продукта должно быть перевезено из Ai в Bj. Обозначим это количество через xij.

Условия а) и б) означают тогда соответственно

.

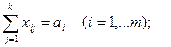
Кроме того xij ³ 0. Общая стоимость перевозок равна .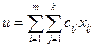

Данную задачу можно рассматривать как задачу принятия решения в усло­виях определенности, в которой в качестве альтернатив выступают неотрицатель­ные m´k-матрицы (xij) удовлетворяющие условиям (а) и (б). Каждой такой матрице соответствует исход – план перевозок, при котором из Ai в Bj перево­зится xij единиц продукта. Целевая функция есть функция u.

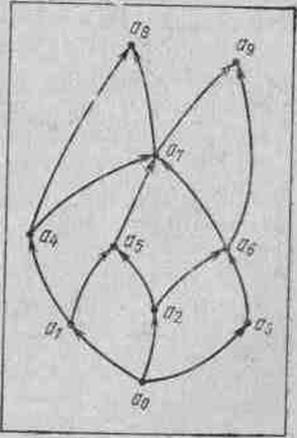
Пример 3-3 (динамическое программирование). Рассмотрим граф (рис. 3-3), каж­дой дуге (х, у) которого приписано положительное число с(х, у). Можно счи­тать, например, что граф представляет собой схему дорог, а с(х, у) – длина пути из х в у. Требуется найти путь из вершины a0 в одну из окончательных вершин (т. е. а8 или a9), имеющий наименьшую общую длину.

Здесь, в отличие от предыдущих двух примеров, мы имеем многошаговую
задачу принятия решения. Действительно, принять решение о выборе пути — зна­чит вначале выбрать первый шаг (т. е. какую-либо дугу, исходящую из а0);
если, например, мы выбрали (а0, а2), то дальше надо производить выбор дуги,
исходящей из a2 и т. д. (разумеется, если из вершины исходит только одна
дуга, то выбор тривиален). Иногда удобнее (как с теоретической, так и с прак­тической точки зрения) представить решение не как последовательный выбор
вершин, а таким образом, что в каждой вершине графа выбирается одна
из исходящих из нее дуг (например, такое представление решения естественно,
если мы не знаем заранее, из какой вершины нам предстоит начать движение).
Тогда выбор альтернативы состоит практически в том, что в каждой вершине
графа отмечается одна из исходящих из нее дуг. Каждой такой сложной альтер­нативе соответствует единственный путь из начальной вершины — путь по отме­ченным дугам; таким образом, усложнив понятие альтернативы, мы снова при­ходим к задаче принятия решения в условиях определенности и с численной оценкой исходов.

При всем различии приведенных выше примеров в них прослеживается одна и та же схема: каждой альтернативе соответствует определенный исход, а «полез­ность» каждого исхода оценивает­ся некоторым числом. Нас здесь интересуют именно численные оценки исходов, поэтому можно установить прямую связь: альтер­натива — численное значение со­ответствующего ей исхода, минуя сами исходы. В итоге получим целевую функцию f, которая опреде­лена теперь на множестве альтернатив. Так как цель состоит здесь в получении исхода, имеющего возможно большее (или возможно меньшее) численное значение, то под оптимальным решением есте­ственно понимать ту альтернативу, которая доставляет целевой функции f наибольшее (или наименьшее) значение.

Таким образом, можно сделать следующий вывод: математиче­ской моделью задачи принятия решения в условиях определенности с численной оценкой исходов является действительная функция, заданная на множестве альтернатив. Нахождение оптимального решения для такой задачи равносильно нахождению экстремума этой функции.

Посмотрим, как в этом случае обстоит дело с существованием оптимальных решений. Если множество альтернатив X конечно (как в примере 4), то целевая функция f принимает конечное чис­ло значений, среди которых будет наибольшее и наименьшее. Если же X бесконечно, то чаще всего в качестве X выступает подмно­жество n-мерного числового пространства Rⁿ. При этом функция f, как правило, является непрерывной, т. е. «близким» альтернативам соответствуют «близ­кие» значения функции f. Как устанавливается в классической тео­реме анализа всякая непрерывная функция, определенная на замкнутой ограниченной области, достигает в этой области наи­большего и наименьшего значения. Сформулированная теорема является тем математическим фундаментом, на котором базиру­ется реализуемость оптимальных решений для данного класса за­дач принятия решений.

Дата добавления: 2015-07-26; просмотров: 262; Нарушение авторских прав

Мы поможем в написании ваших работ!