Вычисление пределов, содержащих иррациональность

Пример 3.1. Вычислить .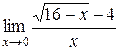

Чтобы избавиться от иррациональности в числителе, умножим числитель и знаменатель дроби на множитель 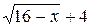. Далее необходимо воспользоваться формулой 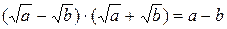. Получим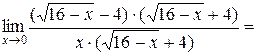

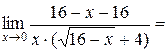
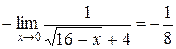
Пример 3.2. Вычислить .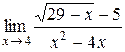

Имеем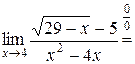

.

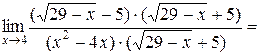
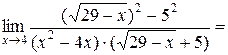
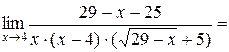
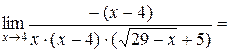
Пример 3.3. Вычислить .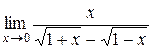

.

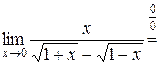
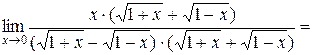
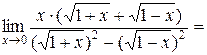
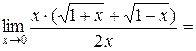
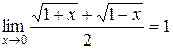Пример 3.4. Найти .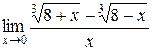

Имеет место неопределённость 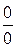. Под знаком предела стоит выражение, содержащее корни третьей степени. Умножим числитель и знаменатель дроби на неполный квадрат суммы, затем воспользуемся формулой

.

Это позволит избавиться от иррациональности в числителе.

.

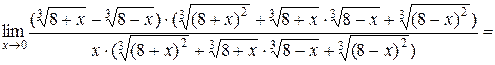
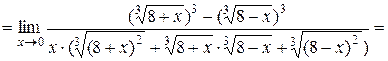
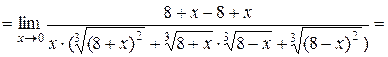
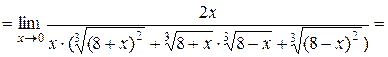
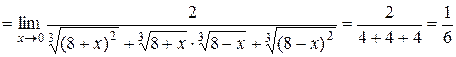Пример 3.5. Вычислить .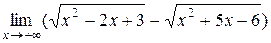

Убеждаемся, что имеет место неопределённость 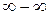. Умножим и разделим на выражение .

.

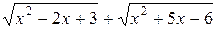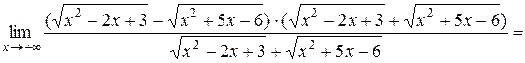
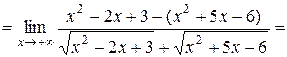
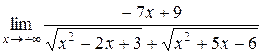Получили неопределённость вида 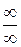, рассмотренную в пункте 1. Необходимо выделить в числителе и в знаменателе дроби старшую степень. .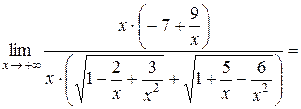

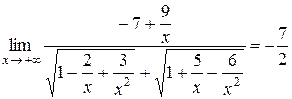Пример 3.6.

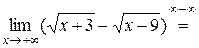
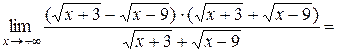
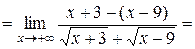
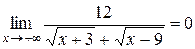, так как числитель –константа, а знаменатель – б.б. функция.

Дата добавления: 2014-02-28; просмотров: 1719; Нарушение авторских прав

Мы поможем в написании ваших работ!