Бесконечно малые величины

Функция a(x) называется бесконечно малой величиной при х ® х₀ или при х ® ¥, если ее предел равен нулю:

a(x) = 0

Связь бесконечно малых величин с пределами функций определяется теоремами:

Теорема: Если f(x) = A, то функцию f(x) можно представить в виде суммы f(x) = A + a(x), где a(x) – бесконечно малая при х ® х₀ (¥).

Обратная теорема: Если функцию f(x) можно представить как сумму числа А и бесконечно малой a(x) при х ® х₀ (¥), то число А есть предел этой функции при х ® х₀ (¥), т.е.

f(x) = A

Свойства бесконечно малых величин:

1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.

2. Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая.

3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.

Замечание. Свойство 3 не рассматривает предел отношения двух бесконечно малых a(x) и b(x) из-за его неопределенности. Этот предел 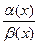может быть равен нулю, числу А ¹ 0 или бесконечности ¥. В первом случае a(x) называется бесконечно малой более высокого порядка малости чем b(x). Это записывается так: a(x) = o(b(x)) при х ® х₀ (¥), т.е. “a(x) есть 0 малое от b(x)”. Во втором случае a(x) и b(x) одного порядка малости (“a(x) есть 0 большое от b(x)” или b (x) = O(a(x))). В третьем случае a(x) более низкого порядка малости чем b(x). При 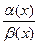=1 a(x) и b(x) называются эквивалентными и пишут a(x) »b(x).

Дата добавления: 2014-02-28; просмотров: 618; Нарушение авторских прав

Мы поможем в написании ваших работ!