Фрагмент программы, реализующий подход №2

Begin

for j:=1 to k do

if(I ³ J) AND (I+j £ k+1) then

if max>a[I,J] then max:=a[I,J];

end;

writeln(‘Максимум элементов заштрихованной области =‘,max);

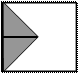Подход №2: организовать перебор только элементов заштрихованной области. Для этого нужно определить границы перебираемой области для каждой строки. Из рисунка матрицы видно, что во всех строках перебор нужно начинать с первого столбца, а заканчивать по-разному: для строк от 1 до 3 заканчивать нужно элементом главной диагонали (у которого I=J), а для строк от 4 до 5 – элементом побочной (I+J=К+1). Поэтому разобьем область на два треугольника:

верхний: строки от 1 до K div 2+1, столбцы от 1 до I-го

нижний: строки от K div 2+2, столбцы от 1 до K+1-I -го

Это и будут параметры вложенных циклов, перебирающих соответствующие элементы. При этом внутри циклов должна выполняться только проверка на максимум.

max:=a[1,1];{начальное значение max=a[1,1], т.к. этот элемент принадлежит области}

for i:=1 to k div 2 + 1 do {для каждой строки верхнего треугольника}

for j:=1 to I do

if max>a[I,J] then max:=a[I,J];

end;

for i:=1 to k div 2 + 2 do {для каждой строки нижнего треугольника}

for j:=1 to k+1-I do

if max>a[I,J] then max:=a[I,J];

end;

writeln(‘Максимум элементов заштрихованной области =‘,max);

Для каждого элемента матрицы делать проверку на принадлежность заштрихованной части. Если проверка дает значение истина, то если сумма цифр четная, то сравнивать элемент с максимумом.

Вспомним, что для максимума нужно задать начальное значение. Теперь мы не знаем, где в заштрихованной области расположен элемент с четной суммой цифр и есть ли он там вообще. Поэтому введем переменную-флажок, которая будет сохранять значение True, пока не найден первый элемент, удовлетворяющий условию, а после его обнаружения будет менять значение на False. Именно этот элемент и будет начальным значение максимума.

Дата добавления: 2014-03-11; просмотров: 322; Нарушение авторских прав

Мы поможем в написании ваших работ!