МЕТОД МОЛЕКУЛЯРНЫХ ОРБИТАЛЕЙ

КОВАЛЕНТНАЯ СВЯЗЬ

Метод МО есть распространенный на молекулы метод атомных орбиталей. Предполагается, что электроны в молекуле находятся на орбиталях, охватывающих все ядра в молекуле.

Для построения волновой функции основного состояния молекулы распределяют все ее электроны по МО с наименьшей энергией по вариационному методу, учитывая ограничения, налагаемые принципом Паули, согласно которому на одной орбитали не может находиться больше двух электронов.

Чаще всего в методе МО применяют приближение ЛКАО для построения МО. Вблизи ядра электроны находятся в поле потенциала, создаваемого в основном этим ядром. Поле, обусловленное другими ядрами, в этой области сравнительно мало. Поэтому, вблизи ядра МО должна быть близка к АО соответствующего атома. Учитывая это, предполагают, что разумное приближение к МО во всех точках пространства можно получить, беря линейную комбинацию атомных орбиталей, относящихся ко всем атомам в молекуле.

y = åc_ij_i

y -МО

j -АО

сi- коэффициенты

Если в это разложение включить достаточно большое число АО,

то, вычисляя коэффициенты на основе вариационного принципа, можно получить хорошее приближение к истинной МО.

Рассмотрим сущность вариационного метода.

Уравнение Шредингера

Нy=Еy

Е- полная энергия молекулы

Умножив обе части на ydt и проинтегрировав получим

E =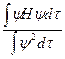

Если волновая функция является одним из решений волнового уравнения, то расчет по этой формуле дает значение дозволенного уровня энергии электрона Е, dt - элемент объема пространства. Если представить искомую волновую функцию в виде

y₁ = c₁j₁ + c₂j₂ + ¼+c_nj_n

то выражение может быть записано

e =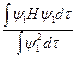

где e меняется в зависимости от выбора y и называется энергетической функцией.

Ввариационном методе исходят из того,что чем меньше энергетическая функция ,тем она ближе к действительному значению энергии основного состояния, а выбранная функция к истинной. Очевидно, что при подстановке уравнение величина энергетической функции будет зависеть от коэффициентов с₁,.с_2, c_n .

Согласно вариационному методу эти коэффициенты нужно выбирать так, чтобы значения энергетической функции были минимальными. Это удобно делать, рассматривая коэффициенты как переменные величины. Тогда условия минимума выразятся системой уравнений

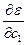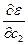= 0 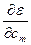= 0 ………= 0

Решение системы уравнений позволяет найти значения с₁,с₂,с_n, при которых энергетическая функция минимальна.

В качестве примера рассмотрим простейшую молекулярную частицу - молекулярный ион водорода Н₂⁺.

Согласно метода ЛКАО молекулярную орбиталь можно представить в виде y = с₁ j_а + с₂ j_в

где а и в - обозначения ядер

Поскольку атомы неразличимы, то плотность вероятности нахождения электрона около каждого из ядер должна быть одной и той же. Это выполняется в случае

с₁² = с₂²

с₁ = с₂ y_g = С_g ( j_a+ j_b )

с₁ = -с₂ y_u = С_u ( j_a - j_b )

y_g - симметричная волновая функция

y_u - антисимметричная волновая функция

Симметричная функция отражает увеличение плотности электронного облака в области перекрывания между двумя атомами по сравнению с плотностью облаков отдельных атомов.

Увеличение плотности отрицательно заряженного электронного облака между положительными ядрами приводит к тому, что ядра как бы стягиваются этим облаком и возникает химическая связь.

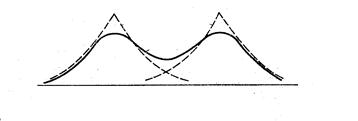
Система электрон в поле двух протонов находится в энергетически более выгодном состоянии Е ,чем исходная система электрон в поле одного протона

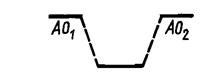
E_g

Поэтому y_g называется связывающей молекулярной орбиталью.

Антисимметричной волновой функции отвечает уменьшение плотности электронного облака между атомами. При этом полoжительно заряженные атомы отталкиваются и система становится неустойчивой.

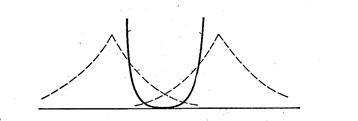
Молекулярной орбитали отвечает энергия большая, чем энергия атома водорода

E_u

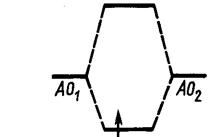
E_g

Орбиталь y_u ,соответствующая повышению энергии, называется

разрыхляющей МО.

Дата добавления: 2014-03-11; просмотров: 435; Нарушение авторских прав

Мы поможем в написании ваших работ!