Схемы и группы соединения обмоток

Принятые ГОСТ схемы соединений обмоток трехфазных двухобмоточных трансформаторов показаны на рис. 4.9. Начала и концы обмоток ВН и НН обозначены согласно сказанному выше.

При построении диаграмм линейные напряжения обмотки ВН (штриховые линии на рис. 4.9) изображаются во всех случаях равносторонними треугольниками напряжений, причем вершины А, В и С находятся соответственно в нижнем левом углу, в верхнем углу и в нижнем правом углу. При этом, говоря о работе трансформаторов, мы должны заранее предусмотреть возможность их параллельной работы, при которой могут быть соединены между собой только равнопотенциальные зажимы. Поэтому одного указания на способ соединения обмоток трансформатора недостаточно; необходимо еще указание на угол сдвига 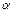между первичным и вторичным линейными напряжениями, в соответствии с чем определяется группа, к которой принадлежит трансформатор.

Покажем, что угол 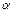зависит от а) направления, в котором намотана обмотка; б) способа обозначения зажимов обмоток, т. е. их маркировки, и в) способа соединения обмоток трехфазных трансформаторов.

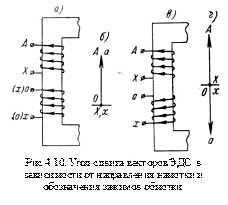
Выясним сначала влияние двух первых факторов на примере однофазного трансформатора. Будем считать, что верхняя обмотка трансформатора на рис. 4.10, a является его первичной обмоткой, а нижняя - вторичной. Предположим, что обе обмотки намотаны в одну и ту же сторону и что их верхние зажимы приняты за начала обмоток и обозначены буквами А и а, а нижние зажимы X и х – за концы обмоток.

Так как обе обмотки трансформатора располагаются на одном и том же стержне и пронизываются одним и тем же основным потоком, то в нашем случае наводимые в обмотках имеют в любой момент времени одинаковое направление относительно зажимов обмоток, например от конца X к началу А в первичной обмотке и от конца х к началу а во вторичной обмотке.

Соответственно этому напряжения 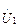и 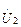на зажимах первичной обмотки и вторичной, приведенной к первичной, обмотки трансформатора совпадают по фазе и изображаются двумя векторами 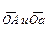, равными по величине и одинаково направленными (рис. 4.10, б).

Если первичная и вторичная обмотки намотаны в разные стороны, но сохраняют те же обозначения зажимов, что и на рис. 4.10, а, то, как это можно видеть на рис. 4.10, в, напряжения 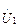и 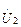относительно за-

жимов первичной и вторичной обмоток направлены в разные стороны,

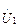например от X к A в первичной обмотке и от а к х во вторичной обмотке. Соответственно этому напряжения и 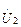должны быть изображены векторами 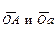, направленными в разные стороны (рис. 4.10, г).

Мы получили бы такой же результат, если бы, оставив тот же способ намотки обмоток, что и на рис. 4.10, а, изменили маркировку вторичной обмотки, поменяв местами обозначения ее зажимов (соответствующие буквы поставлены в скобках на рис. 4.10, а). В этом случае первичное напряжение было бы направлено в одну сторону, например от зажима X к зажиму A, а вторичное напряжение в другую – от зажима а к зажиму х.

Таким образом, принимая вектор 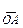первичного напряжения за исходный, мы можем сказать, что вектор 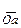вторичного напряжения однофазного трансформатора либо совпадает с вектором 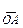по фазе, либо находится с ним в противофазе; в первом случае вектор 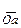смещен относительно вектора 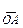на угол 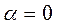°, а во втором – на угол °

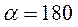Вместо того чтобы выражать угол сдвига между напряжениями в градусах, удобнее пользоваться часовым способом обозначения угла. Для этого вектор 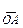первичного линейного напряжения принимают за большую стрелку часов и устанавливают на цифре 12 часового циферблата, а вектор 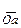вторичного линейного напряжения принимают за малую стрелку часов и устанавливают на циферблате соответственно положению вектора 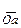относительно вектора 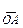.Если векторы 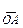и 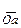совпадают по фазе, как на рис. 4.10, б, то малую стрелку часов мы должны установить, как и большую стрелку, на той же цифре 12 (рис. 4.11). Угол сдвига между стрелками часов равен нулю или, что одно и то же, 360° = 30° 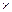12. Здесь угол 30° представляет собой угол между двумя соседними цифрами часового циферблата и принимается за единицу часового сдвига. Цифра 12 и определяет собой группу, к которой в данном случае принадлежит трансформатор.

Если векторы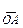и 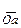находятся в противофазе, как на рис. 4.10, г, то малую стрелку часов мы должны установить на цифре 6 циферблата соответственно углу сдвига на 30° 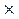6 = 180°. В этом случае группа трансформатора определяется цифрой 6.

Выясним теперь вопрос о группах трехфазных трансформаторов. Предположим, что обе обмотки трансформатора соединены звездой, намотаны в одну и ту же сторону и имеют одинаковые обозначения зажимов. Обмотку ВН мы будем считать первичной обмоткой, а обмотку НН - вторичной. Системы линейных и фазных первичных и вторичных напряжений предполагаются симметричными. Так как вторичная обмотка как бы повторяет первичную, то звезда ах, by и сz вторичных фазных напряжений и треугольник abc вторичных линейных напряжений совпадают соответственно по фазе со звездой АХ, BY и CZ и треугольником ABC фазных и линейных первичных напряжений (рис. 4.12). Таким образом, угол сдвига вторичного линейного напряжения относительно первичного равен нулю, и, следовательно, трансформатор принадлежит к группе (°).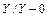

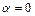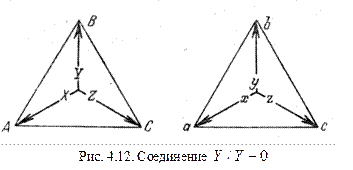
Если мы намотаем обмотку НН в обратном направлении относительно обмотки ВН. или поменяем местами ее начала и концы (но неодновременно одно и другое), то при соединении обеих обмоток по- прежнемузвездой треугольник напряжений abc повернется относительно треугольника ABC на 180°, т. е. на 30° 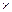6 (рис. 4.13). В этом случае вторую стрелку часов надо установить на цифре 6 циферблата (см. рис. 4.11). Следовательно, данное соединение обмоток относится к группе 6 и пишется в виде .

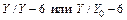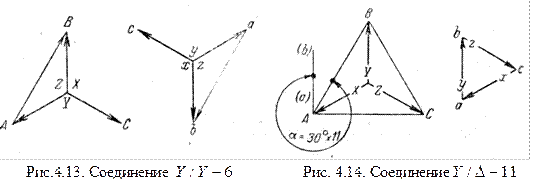
Рассмотрим теперь соединение звезда – треугольник на рис. 4.9, б. Здесь обмотка НН соединена по схеме а—х—с—z—b—y—а. Стороны AB, ВС и СА треугольника напряжений ABC определяют собой линейные напряжения обмотки ВН, а лучи звезды того же треугольника - фазные напряжения этой обмотки. Если обмотки ВН и НН намотаны в одном направлении и имеют одинаковые обозначения зажимов, то векторы фазных напряжений обеих обмоток совпадают. Поэтому при построении треугольника abc нужно провести из точки а (рис. 4.14), находящейся в левом нижнем углу, вектор 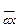параллельно вектору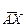, затем из точки с, которую нужно совместить с точкой x, следует провести вектор 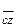параллельно вектору 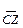и, наконец, из точки b, которую нужно совместить с точкой z, провести вектор 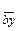параллельно вектору 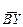, тем самым замыкая треугольник abc. Сопоставляя положения треугольников ABC и abc, например сторон АВ и ab, можно видеть, что второй треугольник повернут относительно первого по направлению вращения часовой стрелки на 330°= 30° 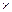11. Следовательно, данное соединение обмоток относится к группе 11 и пишется в виде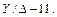

Если бы обмотка НН была намотана в обратном направлении относительно обмотки ВН или мы поменяли местами ее начала и концы, то треугольник abc повернулся бы относительно треугольника ABC на 150° = 30° 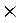5. Следовательно, такое соединение обмоток дает группу 5 и пишется в виде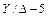. Нетрудно показать, что если бы мы соединили обмотку НН по схеме а–х–b–у–с–z–a, то при одинаковом направлении намотки и одинаковых обозначениях зажимов получили бы группу .

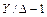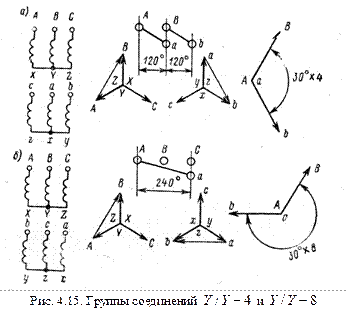
Группы 12, 6, 11 и 5 считаются основными. Из них можно получить ряд производных групп. Для этого нужно только переместить зажимы обмотки НН относительно зажимов обмотки ВН. На рис. 4.15, а обе обмотки соединены звездой и одинаково намотаны, но зажимы а, b, с вторичной обмотки перемещены относительно зажимов А, В, С первичной обмотки на угол 120°; в этом случае треугольник abc повернется относительно треугольника ABC по вращению часовой стрелки на 30° х 4 = 120°, т. е. мы имеем группу соединений.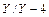

Если бы при соблюдении тех же условий мы переместили зажимы а, b, с относительно зажимов А, В, С на 240° (рис. 4.15, б), то получили бы группу соединений .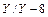

В том случае, когда обмотка НН намотана в обратном направлении относительно обмотки ВН, мы получаем группы 10 и 2 соответственно группам 4 и 8.

Таким образом, при соединении обмоток по схеме звезда - звезда получаются все четные группы соединений. Рассуждая аналогично, нетрудно убедиться, что при соединении обмоток по схеме звезда - треугольник получаются все нечетные группы соединений.

Дата добавления: 2014-03-11; просмотров: 582; Нарушение авторских прав

Мы поможем в написании ваших работ!