Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
ЛЕКЦИЯ 12
Разложение функций по переменным. Минимизация в классе ДНФ.
Основные свойства булевых функций:
1) идемпотентность: хÚх=х, хÙх=х,
2) коммутативность: хÙу=уÙх, хÚу=уÚх,
3) ассоциативность: хÚ(yÚz)= (хÚy)Úz, хÙ(yÙz)= (хÙy)Ùz,
4) поглощение: (xÙy)Úx=x, (xÚy)Ùx=x,
5) дистрибутивность: хÙ(yÚz)= (хÙy)Ú (хÙz), хÚ(yÙz)= (хÚy)Ù (хÚz),
6) 
двойное отрицание: x=x,
7) 
законы де Моргана: хÙу= хÚy, хÙу= хÚy.
8) 
склеивание: xyÚxy=x, (xÚy)(xÚy)=x.
9) действия с константами: xÚ0=x xÙ0=0
xÚ1=1 xÙ1=x
xÚx=1 xÙx=0.
Приоритет: инверсия, конъюнкция, дизъюнкция, остальные функции.
Поскольку свойства определены только для И, ИЛИ, НЕ, то запишем некоторые подстановки (равносильные формулы):
х1® х2= not (х1)or х2
х1¯х2 = not (х1 or х2)
х1|х2= not (х1¯х2)= not (х1 and х2)
х1Å х2 =(not х1 and х2) or ( х1and not х2)
х1Û х2 = not(х1Å х2) =(not х1 or х2) and ( х1or not х2)
х1Å 1 =not х1.
Таким образом, любую переключательную функцию можно задать булевой формулой: с применением переменных, их отрицаний и операций Ú и Ù, т.е <Ú,Ù, not>-сигнатура булевой алгебры.
Для функции f(x1 …xn) можно задать двойственную: f ' (x1 …xn) - двойственная, если f(x1 …xn)= f ' (x1 …xn).
Заметим, что отношение двойственности симметрично.
Любая функция имеет двойственную. Пример:законы де Моргана.
У равных функций двойственные равны.
Функция, двойственная сама себе, называется самодвойственной. Пример:инволютивность, т.е. инверсия самодвойственная.
Принцип двойственности: Если в формуле F, представляющей функцию f, все знаки заменить на знаки двойственных функций, а переменные на их отрицания, то получим формулу F', описывающую функцию f ', двойственную к f.
Для булевой алгебры: конъюнкцию меняем на дизъюнкцию, дизъюнкцию меняем на конъюнкцию, 1 на 0, 0 на 1.
Лемма: (о дизъюнктивном разложении). Любая булева функция f(x1 …xn) может быть представлена в виде дизъюнкции:
f(x1 …xi…xn)= not(xi)f (x1 …,0,…xn) or xif (x1 …,1,…xn).
Док-во: 1) xi=0, f(x1 …xi…xn)= not(0)f (x1 …,0,…xn) or 0f (x1 …,1,…xn)= 1 and f (x1 …,0,…xn) or 0 and f (x1 …,1,…xn)=f (x1 …,0,…xn).
2) xi=1, f(x1 …xi…xn)= not(1)f (x1 …,0,…xn) or 1f (x1 …,1,…xn)= 0 and f (x1 …,0,…xn) or 1 and f (x1 …,1,…xn)=f (x1 …,1,…xn).
Такое представление называется разложением функции по одной переменной.
Существует общий вид разложения функции по m переменным (док-во по индукции)
f(x1 …xi, xi+1 …xn)= or (x1а1 …xiаi f (а1…аi…xn)), где а1…аi=1 or 0.
Пример: f(a b c d).
По переменной а
По переменным а, b
По переменным а, b, c
По переменным а, b,c,d.
Последний расклад - разложение по всем переменным – называется ДНФ.
Опр-е: разложение функции по всем переменным, где каждая переменная или ее отрицание входят в каждую конъюнкту (слагаемое в дизъюнкции), называется СДНФ.
Любая ПФ (кроме тождественного нуля) допускает разложение в СДНФ, причем такое разложение единственно. Из этого следует, что такое разложение позволяет проверять функции на равносильность.
По принципу двойственности формируется понятие КНФ и СКНФ.
Любая ПФ (кроме тождественной единицы) допускает разложение в СКНФ, причем такое разложение единственно.
Если функция задана таблицей истинности, то СДНФ строится по единичному множеству, СКНФ по нулевому.
Из ДНФ СДНФ получается добавлением к каждой неполной конъюнкте единицы (х or (not x)).
ДНФ=not(not(КНФ)) и наоборот.
Однако, СхНФ часто слишком громоздка и неудобна в пользовании, поэтому функцию минимизируют, приводя к МхНФ.
Методы минимизации:
1) метод простых преобразований (метод Квайна). Построен на многократном применении свойств ПФ, чаще всего склеивания и добавления констант.
2) карта Карно: все переменные накладываем на таблицу, применяя закон склеивания две соседние конституенты объединяем в одну, исключив при этом переменную, в которой расходятся оба слагаемых. Краевые ячейки карты считаются соседними. Используя закон идемпотентности, одну и ту же ячейку можно задействовать несколько раз. Склеивать можно только четное число ячеек.
3) метод сочетания индексов. Оформляется в виде таблицы:
список переменных | сочетания переменных | значение функции
В сочетаниях переменных вычеркиваем в каждом столбце сочетания, не соответствующие нужному значению функции. Далее собираются оставшиеся импликанты, выбираются минимальные в каждой строке и из них составляется МНФ - минимальная нормальная форма.
Пример:f=x1 x2 x3 Ú x1 x2 x3 Ú x1 x2 x3 Ú x1 x2 x3 .
Минимизируем в классе ДНФ.
1) сочетание индексов (табл. 4.1):
Таблица 4.1
| x1 | x2 | x3 | x1 x2 | x1 x3 | x2 x3 | x1 x2 x3 | f |
Из первой строки выбираем 00, из четвертой - 011, из пятой - 10.
В итоге имеем: . f= x2 x3 Ú x1 x2 x3 Ú x1 x3 – МДНФ.
2) карта Карно (табл. 4.2):
Таблица 4.2
| Х1 | Х1 |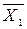 
|
| |
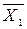
| Х3 | ||||
| ||||
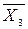
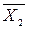
| Х2 | Х2 |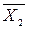
|
Имеем: -00, 1-0, 011, т.е. f= x2 x3 Ú x1 x2 x3 Ú x1 x3 – МДНФ
МКНФ строится по принципу двойственности.
| <== предыдущая страница | | | следующая страница ==> |
| Другие смешанные правовые системы | | | Лекция 13 |
Дата добавления: 2014-03-11; просмотров: 423; Нарушение авторских прав
Мы поможем в написании ваших работ!