
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Подгруппы
|
Читайте также: |
Подмножество 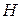 группы
группы 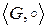 называется ее подгруппой, если
называется ее подгруппой, если 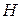 само является группой относительно операции, определенной в группе
само является группой относительно операции, определенной в группе 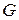 .
.
Теорема (критерий подгруппы). Множество 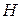 группы
группы 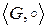 тогда и только тогда является подгруппой, если выполняются два условия:
тогда и только тогда является подгруппой, если выполняются два условия:
а) для любых элементов 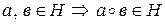 .
.
б) из 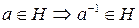 .
.
Справедливость утверждения очевидна. Докажите самостоятельно.
Упр. 9. Доказать, что в группе 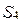 подмножества
подмножества 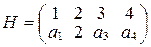 , где
, где 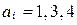 ,
, 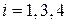 , является ее подгруппой.
, является ее подгруппой.
Упр. 10. Докажите, что в группе 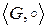 выполняется закон сокращения, т.е. для любых элементов
выполняется закон сокращения, т.е. для любых элементов 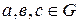 из
из 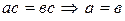 и
и 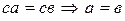 .
.
Упр. 11. Является ли группой относительно сложения: а) множество целых чисел 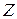 ; б) множество натуральных чисел
; б) множество натуральных чисел 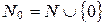 ?
?
Упр. 12. Докажите, что множество всех целых чисел, кратных шести, образует подгруппу 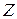 .
.
| <== предыдущая страница | | | следующая страница ==> |
| | | Простейшие свойства кольца |
Дата добавления: 2014-03-11; просмотров: 263; Нарушение авторских прав

Мы поможем в написании ваших работ!