Корреляционные функции сигналов

На практике часто возникает необходимость в характеристике, которая давала бы общее представление об изменении сигнала во времени без разложения его на гармонические составляющие.Подобная «временная» характеристика особенно важна для анализа случайных сигналов и шумов, а также для обнаружения сигналов в шумах, когда решение о наличии сигнала принимается после сличения смеси (сигнал + шум) с заранее известной копией принимаемого сигнала.

В качестве такой временной характеристики широко используется автокорреляционная функция сигнала.

Для детерминированного сигнала s(t) конечной длительности автокорреляционная функция определяется следующим выражением:

(16)

где t - величина временного сдвига сигнала.

Для оценки степени связи между двумя различными сигналами s₁(t) и s₂(t) используется взаимная корреляционная функция, которая определяется выражениями:

(17)

Корреляционная функция стационарного процесса при τ = 0 определяется:

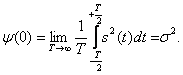(18)

Отсюда видно, что Y(0) совпадает со средней мощностью процесса.

Установление связи между спектральной и корреляционной характеристиками имеет особенно важное значение для сигналов и шумов типа стационарных случайных процессов.

Теорема Винера-Хинчина утверждает, что автокорреляционная функция и энергетический спектр стационарного случайного процесса связаны между собой интегральными преобразованиями Фурье:

(19)

Здесь W₁(w) – энергетический спектр, определяемый на всей оси частот -∞<w<+∞.

Если определять энергетический спектр только на положительной оси частот, имеет место соотношение: 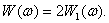При этом

(20)

На основании выражения (20) можно сделать заключение: чем шире энергетический спектр случайного процесса, тем меньше время корреляции и, соответственно, чем больше время корреляции, тем уже спектр процесса.

Дата добавления: 2014-03-13; просмотров: 445; Нарушение авторских прав

Мы поможем в написании ваших работ!