
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Лекция №2 «Главные оси и главные моменты инерции
ПРЕДИСЛОВИЕ
Лекция № 1 «Геометрические характеристики
СОДЕРЖАНИЕ
Северодвинск
Конспект лекций. Часть 2.
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Курзанова Е.В.
Филиал «СЕВМАШВТУЗ» государственного образовательного
Федеральное агентство по образованию Российской Федерации
учреждения высшего профессионального образования «Санкт-
Петербургский государственный морской технический
университет» в г. Северодвинске
УДК 539.3/8
Сопротивление материалов. Конспект лекций. Часть 2/Сост. Е.В.Курзанова, Северодвинск: РИО Севмашвтуза, 2010 - 38 с.
Конспект лекций часть 2 предназначен для студентов всех специальностей, изучающих курс «Сопротивление материалов».
В части 2 конспекта лекций по сопротивлению материалов содержатся основные теоретические положения и зависимости по следующим темам: «Геометрические характеристики плоских сечений», «Кручение», «Срез и смятие».
Рецензенты:
К.т.н., доцент кафедры №3 Н.В.Лобанов,
Генеральный директор ЗАО НТЦ “БАЗИС» В.А. Базанов
Печатается по решению редакционно-издательского совета Севмашвтуза.
© Севмашвтуз, 2010
Предисловие…………………………………………………………………….4
плоских сечений»……………………………………………………………….5
2. Лекция № 2 «Главные оси и главные моменты инерции»..………………………………………….…………………………...13
3. Лекция №3 «Кручение. Расчёты на прочность и жёсткость при кручении»………………………………………………………………………16
4. Лекция №4 «Срез и смятие. Расчёты на прочность»…….………………………………………………………………..32
5. Вопросы для проверки пройденного материала………………………..36
6. Список литературы…………………………………………………………37
В части 2 конспекта лекций содержаться основные теоретические положения и расчётные формулы по следующим темам: Геометрические характеристики плоских сечений, Кручение, Срез и смятие.
Целью конспекта лекций является оказание помощи студентам при изучении предмета, при решении и защите расчетно-графических работ по сопротивлению материалов.
Лекция №1 «Геометрические характеристики плоских сечений»
К геометрическим характеристикам плоских сечений относятся:
· площадь сечения F,
· статические моменты площади Sx , Sy ,
· осевые моменты инерции Jx , Jy ,
· центробежный момент инерции Jxy,
· полярный момент инерции Jρ ,
· момент сопротивления кручению Wρ,
· момент сопротивления изгибу Wx
1.1. Статические моменты площади Sx , Sy
Статический момент площади сечения относительно данной оси равен сумме произведений элементарных площадок на расстояние до соответствующей оси.
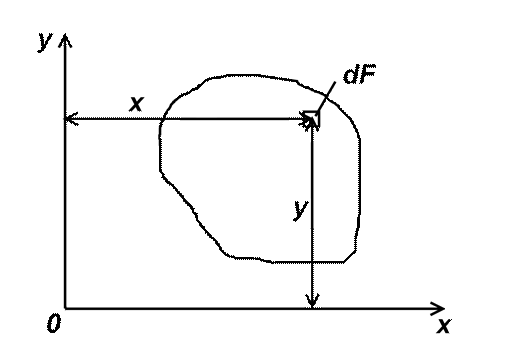
Рис. 1
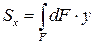 (1)
(1)
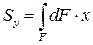 (2)
(2)
Единицы измерения Sxи Sy: [см3], [мм3]. Знак «+» или «-» зависит от расположения осей.
Свойство: Статические моменты площади сечения равны нулю (Sx=0 и Sy=0), если точка пересечения координатных осей совпадает с центром тяжести сечения. Ось, относительно которой статический момент равен, называется центральной. Точка пересечения центральных осей называется центром тяжести сечения.
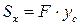
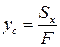 (3)
(3)
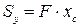
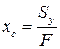 (4)
(4)
Где F - суммарная площадь сечения.
Пример 1:
Определить положение центра тяжести плоского сечения, состоящего из двух прямоугольников с вырезом.
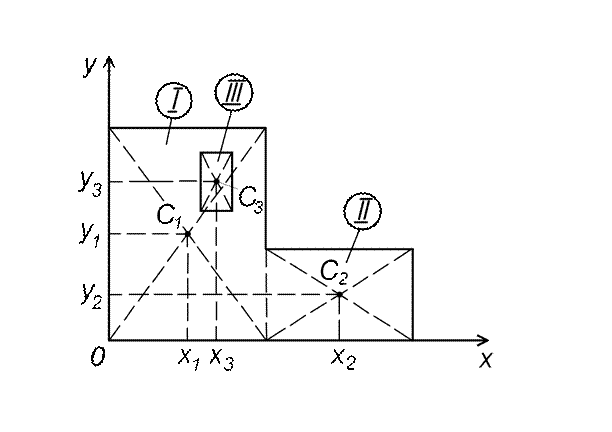
Рис. 2
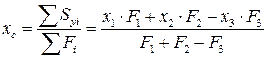 (5)
(5)
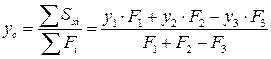 (6)
(6)
Отрицательная площадь вычитается.
1.2. Осевые моменты инерции Jx ; Jy
Осевой момент инерции равен сумме произведений элементарных площадок на квадрат расстояния до соответствующей оси.
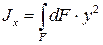 (7)
(7)
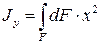 (8)
(8)
Единица измерения [см4], [мм4].
Знак всегда «+».
Не бывает равным 0.
Свойство: Принимает минимальное значение, когда точка пересечения координатных осей совпадает с центром тяжести сечения.
Чем дальше площадь удалена от центральной оси, тем осевой момент инерции сечения больше. Жесткость конструкции повышается.
Осевой момент инерции сечения применяют при расчетах на прочность, жесткость и устойчивость.
1.3. Полярный момент инерции сечения Jρ
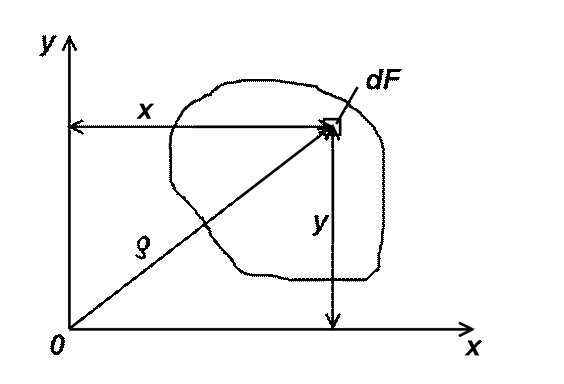
Рис. 3
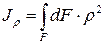 (9)
(9)
Взаимосвязь полярного и осевого моментов инерции:
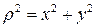 (10)
(10)
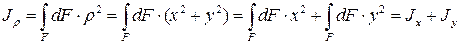
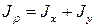 (11)
(11)
Полярный момент инерции сечения равен сумме осевых моментов.
Свойство:
при повороте осей в любую сторону, один из осевых моментов инерции возрастает, а другой убывает (и наоборот). Сумма осевых моментов инерции остается величиной постоянной.
1.4. Центробежный момент инерции сечения Jxy
Центробежный момент инерции сечения равен сумме произведений элементарных площадок на расстояния до обеих осей
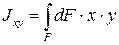 (12)
(12)
Единица измерения [см4], [мм4].
Знак «+» или «-».
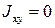 , если координатные оси являются осями симметрии (пример – двутавр, прямоугольник, круг), или одна из координатных осей совпадает с осью симметрии (пример – швеллер).
, если координатные оси являются осями симметрии (пример – двутавр, прямоугольник, круг), или одна из координатных осей совпадает с осью симметрии (пример – швеллер).
Таким образом для симметричных фигур центробежный момент инерции равен 0.
Координатные оси u и v, проходящие через центр тяжести сечения, относительно которых центробежный момент равен нулю, называются главными центральными осями инерции сечения. Главными они называются потому, что центробежный момент относительно них равен нулю, а центральными – потому, что проходят через центр тяжести сечения.
У сечений, не обладающих симметрией относительно осей x или y, например у уголка, 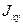 не будет равен нулю. Для этих сечений определяют положение осей u и v с помощью вычисления угла поворота осей x и y
не будет равен нулю. Для этих сечений определяют положение осей u и v с помощью вычисления угла поворота осей x и y
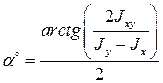 (13)
(13)
Центробежный момент относительно осей u и v - 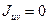
Формула для определения осевых моментов инерции относительно главных центральных осей u и v:
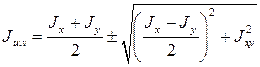 (14)
(14)
где 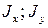 - осевые моменты инерции относительно центральных осей,
- осевые моменты инерции относительно центральных осей,
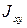 - центробежный момент инерции относительно центральных осей.
- центробежный момент инерции относительно центральных осей.
1.5. Момент инерции относительно оси, параллельной центральной (теорема Штейнера)
Теорема Штейнера:
Момент инерции относительно оси, параллельной центральной, равен центральному осевому моменту инерции плюс произведение площади всей фигуры на квадрат расстояния между осями.
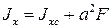 (15)
(15)
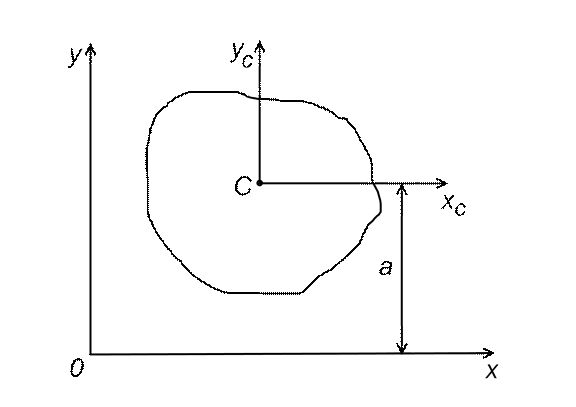
Рис. 4
Доказательство теоремы Штейнера.
Согласно рис. 5 расстояние у до элементарной площадки dF
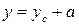
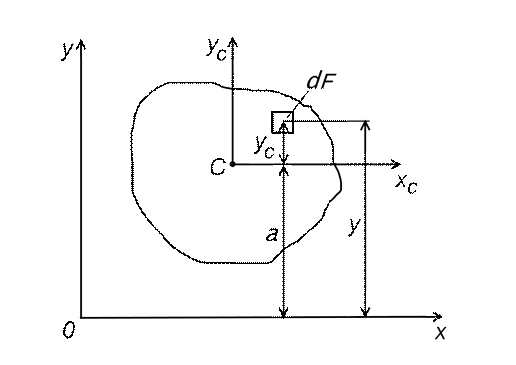
Рис. 5
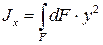
Подставляя значение у в формулу, получим:
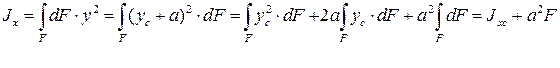
Слагаемое 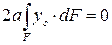 , так как точка С является центром тяжести сечения (см. свойство статических моментов площади сечения относительно центральных осей).
, так как точка С является центром тяжести сечения (см. свойство статических моментов площади сечения относительно центральных осей).
Для прямоугольника высотой h и шириной b :
Осевой момент инерции:
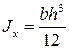
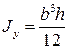
Момент сопротивления изгибу:
момент сопротивления изгибу равен отношению момента инерции к расстоянию наиболее удаленного волокна от нейтральной линии:
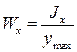
т.к. 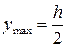 , то
, то 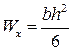
Для круга:
Полярный момент инерции: 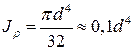
Осевой момент инерции: 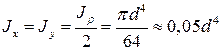
Момент сопротивления кручению: 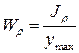
Т.к. 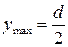 , то
, то 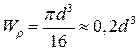
Момент сопротивления изгибу: 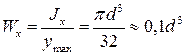
Пример 2. Определить момент инерции прямоугольного сечения относительно центральной оси Сx .
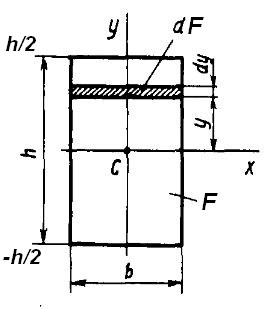
Рис. 6
Решение. Разобьём площадь прямоугольника на элементарные прямоугольники с размерами b (ширина) и dy (высота). Тогда площадь такого прямоугольника (на рис. 6 заштрихована) равна dF=bdy. Вычислим значение осевого момента инерции Jx
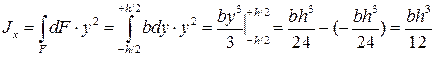
По аналогии запишем
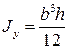 - осевой момент инерции сечения относительно центральной
- осевой момент инерции сечения относительно центральной
оси у
Центробежный момент инерции
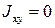 , так как оси Сx и Сy являются осями симметрии.
, так как оси Сx и Сy являются осями симметрии.
Пример 3. Определить полярный момент инерции круглого сечения.
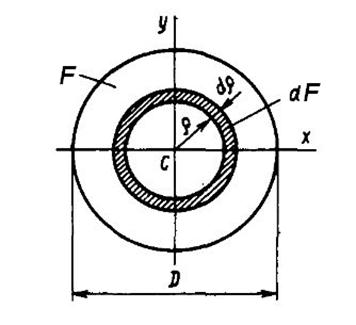
Рис. 7
Решение. Разобьём круг на бесконечно тонкие кольца толщиной 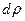 радиусом
радиусом 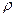 , площадь такого кольца
, площадь такого кольца 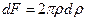 . Подставляя значение
. Подставляя значение 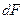 в выражение для полярного момента инерции интегрируя, получим
в выражение для полярного момента инерции интегрируя, получим
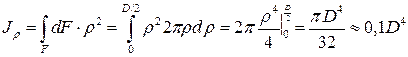
Учитывая равенство осевых моментов круглого сечения 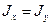 и
и
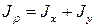 , получаем
, получаем
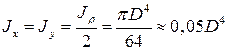
Осевые моменты инерции для кольца равны
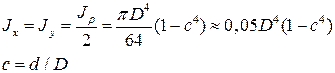
с – отношение диаметра выреза к наружному диаметру вала.
Рассмотрим, как изменяются моменты инерции при повороте координатных осей. Положим, даны моменты инерции некоторого сечения относительно осей 0х, 0у (не обязательно центральных)-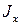 ,
, 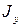 - осевые моменты инерции сечения. Требуется определить
- осевые моменты инерции сечения. Требуется определить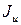 ,
, 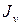 - осевые моменты относительно осей u, v, повёрнутых относительно первой системы на угол
- осевые моменты относительно осей u, v, повёрнутых относительно первой системы на угол 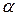 (рис. 8)
(рис. 8)
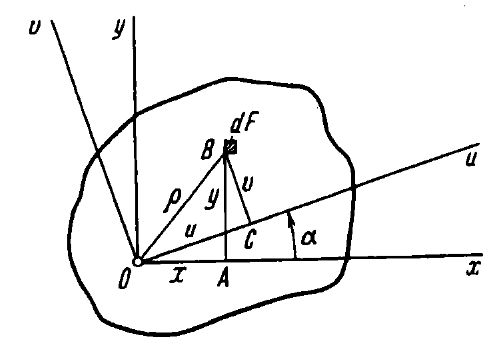
Рис. 8
Так как проекция ломаной линии ОАВС равна проекции замыкающей, находим:
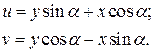 (15)
(15)
Исключим u и v в выражениях моментов инерции:
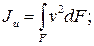
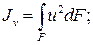
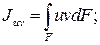
Тогда
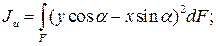
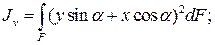
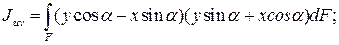
Откуда
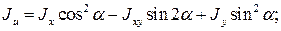 (16)
(16)
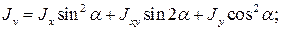 (17)
(17)
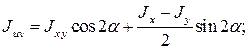 (18)
(18)
Рассмотрим два первых уравнения. Складывая их почленно, получим
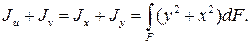
Таким образом, сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей не зависит от угла 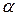 и при повороте осей остается постоянной. Заметим при этом, что
и при повороте осей остается постоянной. Заметим при этом, что
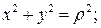
Где 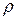 - расстояние от начала координат до элементарной площадки (см. рис.5). Таким образом
- расстояние от начала координат до элементарной площадки (см. рис.5). Таким образом
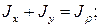
Где 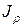 - уже знакомый нам полярный момент инерции:
- уже знакомый нам полярный момент инерции:
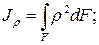
Определим осевой момент инерции круга относительно диаметра.
Так как в силу симметрии 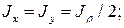 но, как известно,
но, как известно, 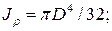
Следовательно, для круга
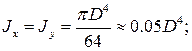
С изменением угла поворота осей 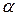 значения моментов
значения моментов 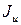 и
и 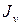 меняются, но сумма остается неизменной. Следовательно существует такое значение
меняются, но сумма остается неизменной. Следовательно существует такое значение 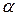 , при котором один из моментов инерции достигает своего максимального значения, в то время как другой момент принимает минимальное значение. Дифференцируя выражение
, при котором один из моментов инерции достигает своего максимального значения, в то время как другой момент принимает минимальное значение. Дифференцируя выражение 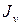 по углу
по углу 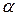 и приравнивая производную к нулю, находим
и приравнивая производную к нулю, находим
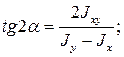 (19)
(19)
При этом значении угла 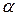 один из осевых моментов будет наибольшим, а другой - наименьшим. Одновременно центробежный момент инерции
один из осевых моментов будет наибольшим, а другой - наименьшим. Одновременно центробежный момент инерции 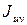 обращается в нуль, что можно легко проверить, приравнивая к нулю формулу для центробежного момента инерции
обращается в нуль, что можно легко проверить, приравнивая к нулю формулу для центробежного момента инерции 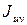 .
.
Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями. Если они к тому же являются центральными (точка начала координат совпадает с центром тяжести сечения), то тогда они называются главными центральными осями (u; v). Осевые моменты инерции относительно главных осей называются главными моментами инерции -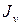 и
и 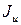
И их значение определяется по следующей формуле:
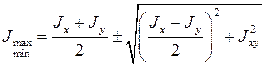 (20)
(20)
Знак плюс соответствует максимальному моменту инерции, знак минус - минимальному.
Существует ещё одна геометрическая характеристика – радиус инерциисечения. Эта величина часто используется в теоретических выводах и практических расчётах.
Радиусом инерции сечения относительно некоторой оси, например 0x, называется величина 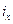 ,определяемая из равенства
,определяемая из равенства
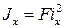 (21)
(21)
F – площадь поперечного сечения,
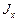 - осевой момент инерции сечения,
- осевой момент инерции сечения,
Из определения следует, что радиус инерции равен расстоянию от оси 0х до той точки, в которой следует сосредоточить (условно) площадь сечения F, чтобы момент инерции одной этой точки был равен моменту инерции всего сечения. Зная момент инерции сечения и его площадь, можно найти радиус инерции относительно оси 0х :
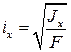 (22)
(22)
Радиусы инерции, соответствующие главным осям, называются главными радиусами инерции и определяются по формулам
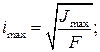
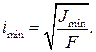 (23)
(23)
| <== предыдущая страница | | | следующая страница ==> |
| | | Основные понятия и зависимости |
Дата добавления: 2014-03-13; просмотров: 1508; Нарушение авторских прав

Мы поможем в написании ваших работ!