
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Обобщенный МНК
|
Читайте также: |
Как и раньше будем предполагать, что среднее значение остаточных величин равно нулю. А дисперсия остатков не остается постоянной для разных значений фактора, а пропорциональна величине
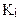 , т.е.
, т.е. 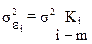 ,
,
где 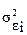 - дисперсия остатков при определенном значении фактора;
- дисперсия остатков при определенном значении фактора;
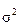 - постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;
- постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;
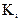 - коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обусловливает неоднородность дисперсии.
- коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обусловливает неоднородность дисперсии.
При этом предполагается, что 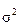 неизвестна, а в отношении величины
неизвестна, а в отношении величины 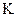 выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности.
выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности.
В общем виде для уравнения 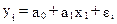 , при
, при 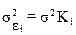 модель примет вид
модель примет вид
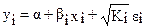 .
.
В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гетероскедастичными остатками, поделив все переменные, зафиксированные в ходе i –ого наблюдения, на 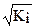 . Тогда дисперсия остатков будет величиной постоянной, т.е.
. Тогда дисперсия остатков будет величиной постоянной, т.е. 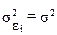 . Т.е. по регрессии y по x мы перейдем к регрессии на новых переменных:
. Т.е. по регрессии y по x мы перейдем к регрессии на новых переменных:
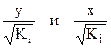 .
.
Уравнение регрессии примет вид:
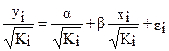 .
.
Исходные данные для данного уравнения будут иметь вид:
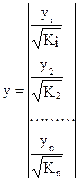
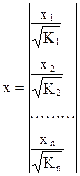
По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешенную регрессию, в которой переменные y и xвзяты с весами 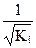 .
.
Оценка параметров нового уравнения с преобразованными переменными приводит к взвешенному методу наименьших квадратов (ВМНК), для которого необходимо минимизировать сумму квадратов отклонений вида
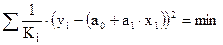 .
.
Соответственно получим следующую систему нормальных уравнений:
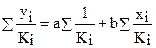
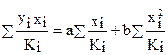 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Предпосылки метода наименьших квадратов | | | Метод наименьших модулей отклонений |
Дата добавления: 2014-03-19; просмотров: 323; Нарушение авторских прав

Мы поможем в написании ваших работ!