Третье уравнение Максвелла – обобщенный закон Гаусса

Поток электрической индукции через любую замкнутую поверхность равен электрическому заряду, заключенному внутри этой поверхности

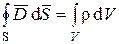. (1.31)

Это соотношение известно из электростатики как теорема Гаусса. Оно было обобщено Максвеллом на случай полей, произвольно зависящих от времени. Уравнение устанавливает, что электрические заряды служат истоками и стоками электрического поля, линии электрической индукции выходят из областей, содержащих положительные заряды, и входят в области, где находятся отрицательные заряды.

Связь между объемной плотностью 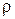электрического заряда и вектором электрической индукции устанавливается обобщенной теоремой Гаусса в дифференциальной форме. Дифференциальную форму теоремы Гаусса можно получить из интегральной, используя теорему Гаусса-Остроградского

. (1.32)

Равенство (1.32) сохраняется при произвольном объеме , следовательно, равны и подынтегральные выражения

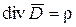. (1.33)

В каждой точке поля дивергенция вектора равна объемной плотности электрического заряда.

Дивергенция вектора есть величина, инвариантная по отношению к преобразованию координат, хотя форма ее записи в разных координатных системах различна. (Величины, не меняющие своего значения при преобразовании координат, называются инвариантными.)

1.3.4. Четвертое уравнение Максвелла –

закон неразрывности магнитных силовых линий

Экспериментально было обнаружено, что силовые линии вектора магнитной индукции 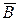независимо от того, создается ли поле постоянными магнитами или катушками с током, образуют в пространстве замкнутые линии. Математически это описывается уравнением

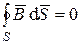. (1.34)

Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. Линии вектора 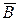замкнуты, либо уходят в бесконечность.

Применяя теорему Гаусса-Остроградского, получаем соотношение (1.34) в дифференциальной форме

,

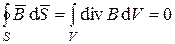откуда

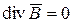. (1.35)

Из сравнения уравнени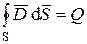й и 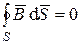вытекает, что магнитные заряды в природе отсутствуют.

Уравнения Максвелла составляют основу всей электродинамики. Из первых двух уравнений следует, что при любом изменении во времени электрического поля возникает вихревое магнитное поле (первое уравнение), любое изменение магнитного поля создает в свою очередь, вихревое электрическое поле (второе уравнение). Таким образом, переменное электрическое и магнитное поля не существуют независимо друг от друга, они непрерывно переходят одно в другое и, как будет показано ниже, образуют электромагнитную волну.

Дата добавления: 2014-10-10; просмотров: 445; Нарушение авторских прав

Мы поможем в написании ваших работ!