Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
Полная система уравнений Максвелла
Уравнения Максвелла описывают электромагнитное поле как форму материи, характеризуемую явлениями, возникающими в пространстве при наличии электрических токов и зарядов. Полная система этих уравнений представлена в таблице 1.1.
Таблица 1.1 - Полная система уравнений Максвелла
| Уравнения Максвелла в дифференциальной форме | Уравнения Максвелла в интегральной форме | Физическое содержание уравнений | |
| I | 
| 
| Токи смещения поля наравне с токами проводимости образуют магнитное поле. |
| II | 
| 
| Переменное магнитное поле образует вихревое электрическое поле. |
| III |
|
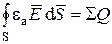
| Электрическое поле может иметь истоки. Истоками электрического поля являются электрические заряды. |
| IV |
|
| Магнитное поле не имеет истоков. В природе свободные магнитные заряды отсутствуют. |
Если параметры среды 
, 
, 
не зависят от напряженностей поля 
и 
, то система уравнений Максвелла будет линейной.
Раздел физики, посвященный изучению переменных электромагнитных полей называется электродинамикой.
| <== предыдущая страница | | | следующая страница ==> |
| Третье уравнение Максвелла – обобщенный закон Гаусса | | | Сторонние силы |
Дата добавления: 2014-10-10; просмотров: 231; Нарушение авторских прав
Мы поможем в написании ваших работ!