Первое уравнение Максвелла – обобщенный закон Ампера

Согласно закону Ампера

.

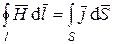В частном случае, если контур в виде окружности охватывает проводник с током , при этом центр окружности совпадает с осью проводника, то вследствие симметрии напряженность магнитного поля одинакова во всех точках контура, то есть не зависит от переменной интегрирования и ее можно вынести за знак интеграла

,

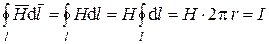откуда

,

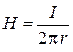где – расстояние от центра проводника до точки наблюдения.

Максвелл обобщил закон Ампера на случай переменного тока. В правой части уравнения он дополнительно ввел слагаемое 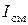, так называемый ток смещения, обусловив это необходимостью сохранения количества электричества в ограниченной системе. Введенное Максвеллом понятие тока смещения, как мы увидим впоследствии, оказалось очень плодотворным. Его величина определяется по формуле, вывод которой приведен ниже

, (1.13)

где – плотность тока смещения.

Таким образом, первое уравнение Максвелла является обобщенным законом Ампера в интегральной форме и записывается следующим образом

. (1.14)

Векторы электромагнитного поля, заряды и токи могут быть связаны между собой либо интегральными соотношениями, либо дифференциальными. Переход от одних соотношений к другим осуществляется с помощью двух теорем векторного анализа: теоремы Остроградского-Гаусса и теоремы Стокса.

Теорема Остроградского-Гаусса связывает интеграл от некоторого векторного поля по замкнутой поверхности с интегралом по объему , ограниченному этой поверхностью, следующим соотношением

. (1.15)

Теорема Стокса связывает интеграл по замкнутому контуру с интегралом по поверхности , ограниченной этим контуром

. (1.16)

Значения дифференциальных операторов дивергенции и ротора в различных координатных системах приводятся в справочниках. Их выражения в декартовой системе координат имеют следующий вид:

;

.

Для получения выражения (1.13), определяющего ток смещения, рассмотрим основные законы электрического тока.

Электрическим током через замкнутую поверхность называется скорость изменения количества электричества 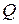в объеме , ограниченном поверхностью , с обратным знаком

. (1.17)

Учитывая, что и , переписываем (1.17)

или, меняя порядок дифференцирования и интегрирования, получаем

.

Преобразуя поверхностный интеграл левой части на основании теоремы Остроградского-Гаусса в интеграл по объему, имеем

.

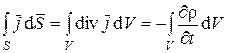Это равенство, справедливое для произвольного объема, может выполняться только в том случае, если равны подынтегральные выражения

. (1.18)

Уравнение (1.18) является дифференциальным выражением уравнения (1.17) и называется уравнением непрерывности тока и заряда.

Истоками линий плотности тока являются те точки поля, где плотность заряда изменяется со временем. Для постоянного тока объемная плотность зарядов 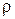в каждой точке среды должна оставаться постоянной, то есть , а это означает, что

. (1.19)

Следовательно,

. (1.20)

Уравнения (1.19) и (1.20) носят название первого закона Кирхгофа в дифференциальной и интегральной формах соответственно. Линии постоянного тока не имеют истоков и стоков. Другими словами, цепь постоянного тока должна быть замкнута. В случае переменного тока линии тока оказались незамкнуты, так как имеют истоки и стоки в точках с изменяющейся плотностью заряда

.

Максвелл обобщил принцип непрерывности линий тока на случай переменного тока путем введения понятия о токе смещения.

Известно (1.5), что

.

Применив к этому равенству теорему Остроградского-Гаусса, получаем

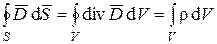или 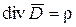. (1.21)

Подставляя (1.21) в (1.18), имеем

.

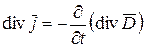Перенося правую часть в левую и меняя порядок дифференцирования по времени и по пространственным координатам, получаем

. (1.22)

Уравнение (1.22) утверждает, что вектор, представляющий собой сумму векторов 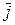и , непрерывен. Другими словами, вектор дополняет вектор плотности тока до замкнутости. Максвелл ввел понятие о плотности тока смещения , понимая под ним второе слагаемое уравнения (1.22)

. (1.23)

По Максвеллу существует полный ток, плотность которого состоит из двух слагаемых: плотности тока проводимости 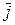, пропорциональной напряженности электрического поля , и плотности тока смещения, пропорциональной производной напряженности поля по времени

.

Таким образом .

Принцип непрерывности линий тока соблюдается и для случая переменного тока. Ток смещения определяется по выражению (1.13)

. (1.24)

Меняя порядок интегрирования и дифференцирования, получаем

. (1.25)

Переход от интегрального уравнения Максвелла (1.14) к дифференциальному может быть осуществлен с помощью теоремы Стокса (1.16)

,

откуда

. (1.26)

Ротор вектора напряженности магнитного поля в любой его точке равен сумме плотности тока проводимости и скорости изменения вектора электрической индукции в этой точке.

Закон Ампера в дифференциальной форме записывается уравнением

. (1.27)

Из уравнения (1.27) на основании формулы векторного анализа вытекает, что дивергенция правой части равенства (1.27) равна нулю, то есть . Между тем, это условие выполняется лишь в частном случае постоянного тока. Для переменных токов закон сохранения количества электричества приводит к требованию, чтобы

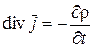. (1.28)

Уравнение (1.27) и равенство (1.28) находятся в очевидном противоречии друг с другом. Не подвергая сомнению закон сохранения количества электричества, мы должны признать несправедливость уравнения (1.27) для переменного поля. Максвелл высказал предположение о том, как надо “исправить” это уравнение для переменных полей. По Максвеллу следует в правую часть уравнения (1.27) вместо плотности тока проводимости поставить плотность полного тока, переписав уравнение (1.27) в виде

,

где – есть сумма векторов плотностей токов проводимости и смещения.

Так как , то это “исправленное” уравнение находится в согласии с законом сохранения количества электричества.

1.3.2. Второе уравнение Максвелла –

обобщенный закон электромагнитной индукции Фарадея

По Фарадею, если через поверхность , ограниченную проводящим контуром , проходит меняющийся по времени магнитный поток, то в контуре возникает электродвижущаяся сила индукции. Обобщение закона по Максвеллу заключается в отказе от ограничения, наложенного на него словами “проводящий” контур. Согласно Максвеллу соотношение

выполняется для всякого контура независимо от того, является ли этот контур проводящим или произвольно выбранным в диэлектрической среде. То есть, меняющееся во времени магнитное поле вызывает (независимо от параметров среды) электрическое вихревое поле.

Поток вектора магнитной индукции 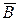по аналогии с потоком 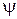вектора электрической индукции можно записать в виде

,

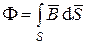тогда второе уравнение Максвелла в интегральной форме – обобщенный закон электромагнитной индукции Фарадея запишется в следующем виде

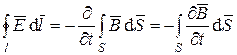. (1.29)

Для перехода к дифференциальной форме применяем теорему Стокса

.

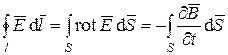Так как – произвольная поверхность, равенство интегралов возможно только при равенстве подынтегральных выражений

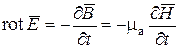. (1.30)

Ротор вектора напряженности электрического поля в любой его точке равен по величине и противоположен по знаку скорости изменения вектора магнитной индукции в этой точке. Таким образом, электрическое поле создается как электрическими зарядами, так и любым изменением во времени вектора магнитной индукции.

Дата добавления: 2014-10-10; просмотров: 609; Нарушение авторских прав

Мы поможем в написании ваших работ!