
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Тезисы к лекции
Сверточные коды
Сверточные коды (СК) относятся к непрерывным кодам. Здесь нет деления на кодовые комбинации как в блочных. Выходные элементы, в данном случае, зависят от ряда предшествующих информационных элементов.
Свёрточный код описывается тремя целыми числами (n, k,K).
Отношение имеет такой же смысл скорости кода, как и для блочного, но n не определяет длину блока. В данном случае k элементов, поступающих в кодер, порождают n элементов на его выходе. K – длина кодового ограничения, оно определяется числом разрядов (ячеек памяти) в кодирующем регистре сдвига. Кодовое ограничение определяет мощность и сложность кода.
Выходные элементы СК зависят не только от текущего входного элемента, но и от (K-1) предыдущих, т.е. СК имеет память.
Основными элементами сверточного кода являются: регистр сдвига, сумматор по модулю 2, коммутатор.
Регистр сдвига (англ. Shift register) – это динамическое запоминающее устройство, хранящее двоичные символы 0 и 1. Память кода определяет число триггерных ячеек m в регистре сдвига. Когда на вход регистра сдвига поступает новый информационный символ, то символ, хранящийся в крайнем правом разряде, выводится из регистра и сбрасывается. Остальные символы перемещаются на один разряд вправо и, таким образом, освобождается крайний левый разряд куда будет поступать новый информационный символ.
Сумматор по модулю 2 осуществляет сложение поступающих на него символов 1 и 0. Правило сложения по модулю 2 таково: сумма двоичных символов равна 0, если число единиц среди поступающих на входы символов четно, и равно 1, если это число нечетно.
Коммутатор последовательно считывает поступающие на его входы символы и устанавливает на выходе очередность кодовых символов в канал связи. По аналогии с блоковыми кодами, сверточные коды можно классифицировать на систематические и несистематические.
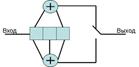
Рисунок 8.1. Простейший сверточный код (2.1.3)
Параметры и характеристики сверточных кодов
Значения выходного вектора для текущего элемента и предшествующих, можно найти поразрядно суммируя (по модулю два) коэффициенты ячеек, содержащих единицы.
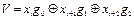
Матицы коэффициентов и полиномов являются взаимно транспонированными. В этом случае выходной вектор можно получить путем умножения входного вектора на транспонированную матрицу полиномов
При сверточном кодировании преобразование информационных последовательностей в выходные и кодовые происходит непрерывно.
Число информационных символов, поступающих за один такт на вход кодера - k.
Число символов на выходе кодера - n, соответствующих k, поступившим на вход символам в течение такта.
Скорость кода определяется отношением R=k/n и характеризует избыточность, вводимую при кодировании. Избыточность кода J = 1 - R
Память кода (входная длинна кодового ограничения или информационная длина кодового слова), определяется максимально степенью порождающего многочлена в составе порождающей матрицы
Вес w двоичных кодовых последовательностей определяется числом "единиц", входящих в эту последовательность или кодовые слова.
Диаграмма состояний кодера
Сверточный кодер принадлежит к классу устройств называемых конечными автоматами. Конечные автоматы это системы обладающие памятью о прошлых событиях (сигналах). При этом число состояний, в которых может находиться система - конечно. Состояние отражает информацию о прошлых событиях и определяет возможное поведение системы в будущем.
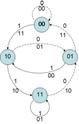
Рисунок 8.2. Диаграмма состояний кодера сверточного кода (2.1.3)
Состояние должно содержать минимум информации о прошлом на основание которой, совместно с текущими входными данными можно определить данные на выходе.
Из каждого текущего состояния возможны переходы лишь в некоторые из состояний и не возможны в другие.
Для СК со скоростью 1/n, состояний могут быть представлены содержимым (К-1) младших ячеек регистра. Поступление следующего элемента будет определять как переход в следующее состояние, так и элементы на выходе кодера.
Оценка исправляющей способности сверточного кода
Для блочных кодов исправляющая способность есть номинальное количество ошибок в блоке длиной n, которое может быть гарантированно исправлено. Данная способность однозначно определяется кодовым расстоянием:
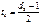
Для СК исправляющая способность не может быть задана так однозначно. Данная способность определяется через просвет или свободное расстояние кода по аналогичной формуле (8.1):
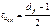
 (8.1)
(8.1)
где df - просвет или свободное расстояние кода.
 При декодировании по принципу максимального правдоподобия СК способен исправить заданное количество ошибок в пределах нескольких длин кодовых ограничений («несколько» - это от 3 до 5 К). Точное значение зависит от распределения ошибок.
При декодировании по принципу максимального правдоподобия СК способен исправить заданное количество ошибок в пределах нескольких длин кодовых ограничений («несколько» - это от 3 до 5 К). Точное значение зависит от распределения ошибок.
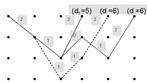
Просветом или свободным расстоянием называется минимальный вес пути, начинающегося и заканчивающегося в нулевом состоянии.
1) 100 d=5
2) 1100 d=6
3) 10100 d=6
Рисунок 8.3. Определение веса пути
Для кода (2.1.3) минимальный просвет df =5, значит он может исправить две любые ошибки.
Сверточные коды используемые в системах связи
В GSM используют код (2.1.5) с полиномами: df = 7
g1(x)=1+x3+x4
g2(x)=1+x+x3+x4
В системах спутниковой связи (2.1.7): df = 10
g1(x)=1+x2+x3+x5+x6
g2(x)=1+x+x2+x3+x6.
Декодирование сверточных кодов. Алгоритм декодирования Витерби.
Задача декодирования сверточного кода заключается в выборе пути вдоль решетки наиболее похожего на принятую последовательность.
Каждый путь вдоль решетчетой диаграммы складывается из ветвей соединяющих узлы. Каждой ветви решетки соответствует кодовое слово из двух бит. Каждую ветвь на каждом периоде можно пометить расстоянием Хемминга между полученным кодовым словом и кодовым словом, соответствующим ветви. Складывая расстояния Хемминга ветвей, составляющих путь, получим метрику соответствующего пути.
Данная метрика будет характеризовать степень подобия каждого пути принятой последовательности. Чем меньше метрика, тем более похожи путь и принятая последовательность. Т.о. результатом декодирования будет информационная последовательность, соответствующая пути с минимальной метрикой.
Если в одно и тоже состояние входят два пути выбирается тот, который имеет лучшую метрику. Такой путь называется выжившим. Отбор выживших путей проводится для каждого состояния.
Систематические и несистематические сверточные коды.
Систематически сверточный код – это код, содержащий в своей выходной последовательности кодовых символов породившую ее последовательность информационных символов. Иначе код называют несистематическим.
У систематических кодов при той же длине кодового ограничения и скорости кода свободное расстояние меньше. А значит, меньше и исправляющая способностью.
Жесткая и мягкая схемы принятия решения
В зависимости от того в какой форме информация поступает с выхода УПС в декодер СК различают жесткую и мягкую схему принятия решения.
Если решение о значащей позиции принимается жестко «1» или «0» – это жесткая схема.
Если УПС выдает декодеру значение квантованное более чем на 2 уровня – мягкое декодирование.
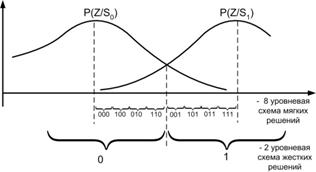 |
Мягкая схема обеспечивает декодер большим количеством информации для принятия решения. Вместе с решением о значащей позиции передается и мера его достоверности.
Рисунок 8.4. Жесткая и мягкая схемы декодирования
Дата добавления: 2014-03-22; просмотров: 582; Нарушение авторских прав

Мы поможем в написании ваших работ!