
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Тезисы к лекции. Широкое распространение на практике получил класс линейных кодов, которые называются циклическими
Циклический код
Широкое распространение на практике получил класс линейных кодов, которые называются циклическими. Данное название происходит от основного свойства этих кодов: если некоторая кодовая комбинация принадлежит циклическому коду, то комбинация, полученная циклической перестановкой исходной комбинации (циклическим сдвигом), также принадлежит данному коду.
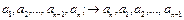 .
.
Вторым свойством всех разрешенных комбинаций циклических кодов является их делимость без остатка на некоторый выбранный полином, называемый производящим.
Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на производящий полином.
В теории циклических кодов кодовые комбинации обычно представляются в виде полинома. Так, n-элементную кодовую комбинацию можно описать полиномом (n-1) степени, в виде
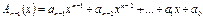 (7.1)
(7.1)
где ai={0,1}, причем ai=0 соответствуют нулевым элементам комбинации, а ai=1 - ненулевым.
Запишем полиномы для конкретных 4-элементных комбинаций
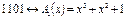
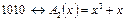
Действия над многочленами
При формировании комбинаций циклического кода часто используют операции сложения многочленов и деления одного многочлена на другой.
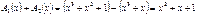 ,
,
Поскольку 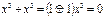 .
.
Следует отметить, что действия над коэффициентами полинома (сложение и умножение) производятся по модулю 2.
Рассмотрим операцию деления на следующем примере:
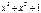


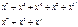
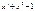

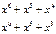

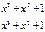
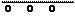 |
Деление выполняется, как обычно, только вычитание заменяется суммированием по модулю два.
Отметим, что запись кодовой комбинации в виде многочлена, не всегда определяет длину кодовой комбинации. Например, при n = 5, многочлену 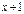 соответствует кодовая комбинация 00011.
соответствует кодовая комбинация 00011.
Алгоритм получения разрешенной кодовой комбинации циклического кода из комбинации простого кода
Пусть задан полином 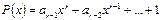 , определяющий корректирующую способность кода и число проверочных разрядов r, а также исходная комбинация простого k-элементного кода в виде многочлена
, определяющий корректирующую способность кода и число проверочных разрядов r, а также исходная комбинация простого k-элементного кода в виде многочлена 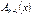 .
.
Требуется определить разрешенную кодовую комбинацию циклического кода (n, k).
1. Умножаем многочлен исходной кодовой комбинации на 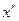
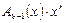
2. Определяем проверочные разряды, дополняющие исходную информационную комбинацию до разрешенной, как остаток от деления, полученного в предыдущем пункте произведения на образующий полином
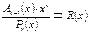
3. Окончательно разрешенная кодовая комбинация циклического кода определится так
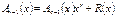
Для обнаружения ошибок в принятой кодовой комбинации достаточно поделить ее на производящий полином. Если принятая комбинация - разрешенная, то остаток от деления будет нулевым. Ненулевой остаток свидетельствует о том, что принятая комбинация содержит ошибки. По виду остатка (синдрома) можно в некоторых случаях также сделать вывод о характере ошибки, ее местоположении и исправить ошибку.
Формирование базиса (производящей матрицы) циклического кода
Формирование базиса циклического кода возможно как минимум двумя путями.
Вариант первый.
1. Составить единичную матрицу для простого исходного кода.
2. Определить для каждой кодовой комбинации исходного кода группу проверочных элементов и дописать их в соответствующие строки матрицы.
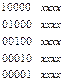
Полученная матрица и будет базисом циклического кода. Причем, в данном случае, разрешенные комбинации заведомо разделимы (т.е. информационные и проверочные элементы однозначно определены).
Вариант второй.
1. Дописать слева от КК, соответствующей образующему полиному циклического кода нули так, чтобы длина разрешенной кодовой комбинации равнялась n.
2. Получить остальные разрешенные кодовые КК базиса, используя циклический сдвиг исходной. (В базисе должно быть k – строк). В данном случае код будет неразделимым.
Получив базис ЦК, можно получить все разрешенные комбинации, проводя сложение по модулю 2 кодовых комбинаций базиса в различных сочетаниях и плюс нулевая.
Циклические коды достаточно просты в реализации, обладают высокой корректирующей способностью (способностью исправлять и обнаруживать ошибки) и поэтому рекомендованы МСЭ-Т для применения в аппаратуре ПД. Согласно рекомендации V.41 в системах ПД с ОС рекомендуется применять код с производящим полиномом
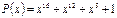
Построение кодера циклического кода
Рассмотрим код (9,5) образованный полиномом
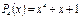 .
.
Разрешенная комбинация циклического кода 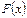 образуется из комбинации простого (исходного) кода путем умножения ее на
образуется из комбинации простого (исходного) кода путем умножения ее на 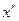 и прибавления остатка R(x) от деления
и прибавления остатка R(x) от деления 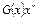 на образующий полином
на образующий полином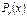 .
.
1. Умножение полинома на одночлен 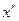
эквивалентно добавлению к двоичной последовательности соответствующей G(x) , r - нулей справа.
Пусть 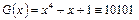
тогда 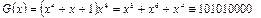

Для реализации операции добавления нулей используется r-разрядный регистр задержки.
2. Рассмотрим более подробно операцию деления:

Как видим из примера, процедура деления одного двоичного числа на другое сводится к последовательному сложению по mod2 делителя [10011] с соответствующими членами делимого [10101], затем с двоичным числом, полученным в результате первого сложения, далее с результатом второго сложения и т.д., пока число членов результирующего двоичного числа не станет меньше числа членов делителя.
Это двоичное число и будет остатком 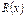 .
.
Построение формирователя остатка циклического кода
Структура устройства осуществляющего деление на полином полностью определяется видом этого полинома. Существуют правила позволяющие провести построение однозначно.
Сформулируем правила построения ФПГ.
1. Число ячеек памяти равно степени образующего полинома r.
2. Число сумматоров на единицу меньше веса кодирующей комбинации образующего полинома.
3. Место установки сумматоров определяется видом образующего полинома.
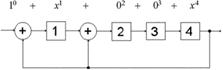
Сумматоры ставят после каждой ячейки памяти, (начиная с нулевой) для которой существует ненулевой член полинома. Не ставят после ячейки для которой в полиноме нет соответствующего члена и после ячейки старшего разряда.
4. В цепь обратной связи необходимо поставить ключ, обеспечивающий правильный ввод исходных элементов и вывод результатов деления.
Структурная схема кодера циклического кода
Полная структурная схема кодера содержит регистр задержки и формирователь проверочной группы.
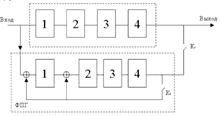
Работа схемы для кодера (n, k)
1. На первом этапе К1– замкнут К2 – разомкнут. Идет одновременное заполнение регистров задержки и сдвига информационными элементами (старший вперед!) и через k-1 тактов старший разряд в последней ячейке (под номером k-1)
2. Во время k-го такта К2 – замыкается, а К1 – размыкается с этого момента в ФПГ формируется остаток. Одновременно из РЗ на выход выталкивается задержание информационные разряды.
За k тактов (с k по n включительно) в линию уйдут все k -информационных элемента. К этому времени в ФПГ сформируется остаток
3. К2 – размыкается, К1 – замыкается, и в след за информационными в линию уйдут элементы проверочной группы.
4. Одновременно идет заполнение регистров новой комбинацией.
Второй вариант построения кодера ЦК.
Рассмотренный выше кодер очень наглядно отражает процесс деления двоичных чисел. Однако можно построить кодер содержащий меньшее число элементов т.е. более экономичный.
Устройство деления на производящий полином 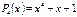 можно реализовать в следующем виде:
можно реализовать в следующем виде:
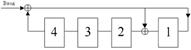
За пять тактов в ячейках будет сформирован такой же остаток от деления, что и в рассмотренном выше Формирователе проверочной группы. (ФПГ).
За эти же 5 тактов информационные разряды, выданные сразу на модулятор.
Далее в след за информационными уходят проверочные из ячеек устройств деления.
Но важно отключить обратную связь на момент вывода проверенных элементов, иначе они исказятся.
Окончательно структурная схема экономичного кодера выглядит так.
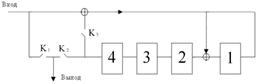
- На первом такте Кл.1 и Кл.3 замкнуты, информационные элементы проходят на выход кодера и одновременно формируются проверочные элементы.
- После того, как в линию уйдет пятый информационный элемент, в устройстве деления сформируются проверочные;
- на шестом такте ключи 1 и 3 размыкаются (разрываются обратная связь), а ключ 2 замыкается и в линию уходят проверочные разряды.
Ячейки при этом заполняются нулями и схема возвращается в исходное состояние.
Определение ошибочного разряда в ЦК.
Определение ошибочного разряда в ЦК
Пусть А(х) - многочлен соответствующий переданной кодовой комбинации. Н(х) - многочлен соответствующей принятой кодовой комбинацией.
Тогда сложение данных многочленов по модулю два даст многочлен ошибки.
E(x)=A(x)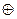 H(x)
H(x)
При однократной ошибке Е(х) будет содержать только один единственный член соответствующий ошибочному разряду.
Остаток – полученный от деления принятого многочлена H(x) на производящей Pr(x) равен остатку, полученному при делении соответствующего многочлена ошибок E(x) на Pr(x)
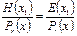
При этом ошибке в каждом разряде будет соответствовать свой остаток R(x) (он же синдром), а значит, получив синдром можно однозначно определить место ошибочного разряда.
Алгоритм определения ошибки
Пусть имеем n-элементные комбинации (n = k + r) тогда:
1. Получаем остаток от деления Е(х) соответствующего ошибке в старшем разряде, на образующей поленом Pr(x)

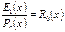
2. Делим полученный полином Н(х) на Pr(x) и получаем текущий остаток R(x).
3. Сравниваем R0(x) и R(x).
- если они равны, то ошибка произошла в старшем разряде.
- если "нет", то увеличиваем степень принятого полинома на Х и снова проводим деления
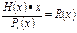
4. Опять сравниваем полученный остаток с R0(x)
- если они равны, то ошибки во втором разряде.
- если нет, то умножаем Н(х)х2 и повторяем эти операции до тех пор, пока R(X) не будет равен R0(x).
Ошибка будет в разряде соответствующем числу на которое повышена степень Н(х) плюс один.
Например: 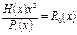 то номер ошибочного разряда 3+1=4
то номер ошибочного разряда 3+1=4
Пример декодирования комбинации ЦК.
Положим, получена комбинация H(х)=111011010
Проанализируем её в соответствии с вышеприведенным алгоритмом.
Реализуя алгоритм определения ошибок, определим остаток от деления вектора соответствующего ошибке в старшем разряде Х8 на производящий полином P(x)=X4+X+1
X8 X2+X+1
X8+X5+X4 x4+x+1
X5+X4
X5+X2+X
X4+X2+X
X4+X+1
X2+1=R0(X)=0101
Разделим принятую комбинацию на образующий полином

Полученный на 9-м такте остаток, как видим, не равен R0(X). Значит необходимо умножить принятую комбинацию на Х и повторить деление. Однако результаты деления с 5 по 9 такты включительно будут такими же, значит необходимо продолжить деление после девятого такта до тех пор, пока в остатке не будет R0(Х). В нашем случае это произойдет на 10 такте, при повышении степени на 1. Значит ошибки во втором разряде.
Декодер циклического кода с исправлением ошибки
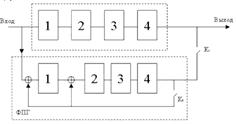
Если ошибка в первом разряде, то остаток R0(X)=10101 появления после девятого такта в ячейках ФПГ.
Если.во втором по старшинству то после 10го;
в третьем по старшинству то после 11го;
в четвертом по старшинству то после 12го
в пятом по старшинству то после 13го
в шестом по старшинству то после 14го
в седьмом по старшинству то после 15го
в восьмом по старшинству то после 16го
в девятом по старшинству то после 17го.
На 10 такте старший разряд покидает регистр задержки и проходит через сумматор по модулю 2.
Если и этому моменту остаток в ФПГ=R0(X), то логическая 1 с выхода дешифратора поступит на второй вход сумматора и старший разряд инвертируется.
В нашем случае инвертируется второй разряд на 11 такте.
Выбор образующего полинома
В теории циклических кодов показано, что образующий полином представляет собой произведение так называемых минимальных многочленов mi(x), являющихся простыми сомножителями (то есть делящимся без остатка лишь на себя и на 1) бинома xn+ 1:
P(x)=m1(x)* m3(x)…mj(x), (7.2)
где j = d0 – 2 =( 2tu.ош+1) – 2 = 2 tи.ош – 1.
Существуют специальные таблицы минимальных многочленов, одна из которых приведена ниже. Кроме образующего полинома необходимо найти и количество проверочных разрядов r. Оно определяется из следующего свойства циклических кодов: для любых значений l и tи.ош существует циклический код длины n =2l – 1, исправляющий все ошибки кратности tи.ош и менее, и содержащий не более 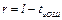 проверочных элементов.
проверочных элементов.
Так как 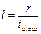 , то
, то 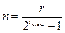 откуда
откуда 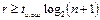 .
.
Очевидно, что для уменьшения времени передачи кодовых комбинаций, r следует выбирать как можно меньше.
После определения количества проверочных разрядов r, вычисления образующего полинома удобно осуществить, пользуясь таблицей минимальных многочленов, представленной в следующем виде:
Таблица 7.1 - Выбор образующего полинома
| J=2tи.ош -1 | Вид минимальных многочленов для | |||||
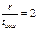
| 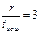
| 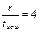
| 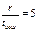
| 
| 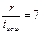
| |
| x2+x+1 | x3+x+1 | x4+x+1 | x5+x+1 | x6+x+1 | x7+x+1 | |
| - | - | x4+x3+x2+x+1 | x5+x4+x3+x2+1 | x6+x4+x2+x+1 | x7+x3+x2+x+1 | |
| - | - | - | x5+x4+x2+x+1 | x6+x5+x2+x+1 | x7+x4+x3+x2+1 | |
| - | - | - | - | x6+x3+1 | х7+x6+x5+x4+x2+x+1 |
Определяя образующий полином, нужно из столбца для соответствующего соотношения 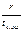 выписать все многочлены, начиная с верхней строки до нижней с номером j=2tи.ош–1 включительно. После этого следует перемножить выбранные минимальные многочлены в соответствии с (*). В частности, если r=3, tи.ош=1, j=2*1-1=1, образующий полином будет представлять собой единственный минимальный многочлен P(x)= m1(x) = x3+x+1 (первая строка, второй столбец таблицы ). Соответственно образующее число равно 1011.
выписать все многочлены, начиная с верхней строки до нижней с номером j=2tи.ош–1 включительно. После этого следует перемножить выбранные минимальные многочлены в соответствии с (*). В частности, если r=3, tи.ош=1, j=2*1-1=1, образующий полином будет представлять собой единственный минимальный многочлен P(x)= m1(x) = x3+x+1 (первая строка, второй столбец таблицы ). Соответственно образующее число равно 1011.
Лекция №8. Свёрточные коды. Декодирование свёрточных кодов. Алгоритм декодирования Витерби.
| <== предыдущая страница | | | следующая страница ==> |
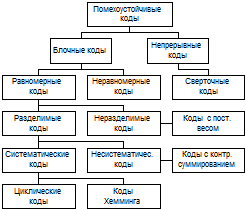
| Тезисы к лекции. Помехоустойчивые коды делятся на блочные и непрерывные коды | | | Тезисы к лекции |
Дата добавления: 2014-03-22; просмотров: 480; Нарушение авторских прав

Мы поможем в написании ваших работ!