Тезисы к лекции. Помехоустойчивые коды делятся на блочные и непрерывные коды

Классификация кодов.

Помехоустойчивые коды делятся на блочные и непрерывные коды. К блочным кодам относятся коды, в которых каждому сообщению отводится блок из n символов (разрядов) или блоки с разным числом символов. В связи с этим блочные коды делятся на равномерные и неравномерные коды. Широкое практическое применение нашли равномерные коды. К неравномерным кодам относится, например, код Морзе. Непрерывные коды, к которым относятся рекуррентные (свёрточные), представляют собой непрерывные последовательности единичных элементов, не разделенные на блоки. В таких кодах избыточные разряды помещаются в определенном порядке между информационными.

Равномерные блочные коды делятся на разделимые и неразделимые коды. Разделимые коды в свою очередь делятся на систематические (линейные) и несистематические (нелинейные) коды. Код называется линейным, если любая разрешенная КК может быть получена в результате линейной операции под набором не нулевых линейно-независимыми КК. В систематических кодах проверочные элементы формируются линейным преобразованием информационных.

Нелинейные коды указанным выше свойством не обладают и применяются значительно реже. Примером несистематического кода является код с контрольным суммированием.

Различают два метода формирования проверочной группы: поэлементной и в целом; последний характерен для широко распространенных полиномиальных кодов (и их разновидности – циклических). Среди систематических кодов большое применение нашли коды Хэмминга. Эти коды, обеспечивающие d₀=3, позволяют исправить одну ошибку. Помехоустойчивые коды могут иметь основание (значность) и больше 2. Однако в связи со сложностью построения кодирующих и декодирующих устройств они на практике применяются значительно реже двоичных.

Рисунок 5.1. Классификация помехоустойчивых кодов

Линейные коды.

Двоичный блочный код является линейным, если сумма по модулю 2 двух кодовых слов является также кодовым словом.

Линейные коды также называют групповыми.

Понятие группы.

Множество элементов с определенной на нем групповой операцией называется группой, если выполняется следующие условия:

1. Замкнутость g_i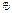g _j= g_k 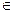G в результате операции с двумя элементами группы получается третий, так же принадлежащий этой группе.

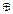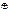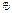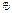2. Ассоциативность (сочетательность) (g_ig_j) g_k = g_i(g_j g_k)

3. Наличие нейтрального элемента g_j 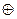e = g_j

4. Наличие обратного элемента g_i 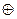(g_i)^-1= e

Если выполняется условие g_i 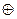g_j = g_j 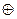g_i, то группа называется коммутативной.

Множество кодовых комбинаций n-элементного кода является замкнутой группой с заданной групповой операцией сложение по модулю 2.

Поэтому, используя свойство замкнутости относительно операции 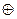2, множество всех элементов можно задать не перечислением всех элементов, а производящей матрицей.

Все остальные элементы, кроме 0, могут быть получены путем сложения по модулю 2 строк производящей матрицы в различных сочетаниях.

В общем случае строки производящей матрицы могут быть любыми линейно независимыми, но проще и удобнее брать в качестве производящей матрицы – единичную.

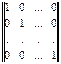
Лекция №7. Циклические коды. Декодирование циклических кодов.

Дата добавления: 2014-03-22; просмотров: 243; Нарушение авторских прав

Мы поможем в написании ваших работ!